Règle du trapèze

La méthode des trapèzes est une méthode numérique simple pour calculer une valeur approchée d’une intégrale définie. Elle repose sur l’idée de remplacer la courbe d’une fonction par des segments de droite, afin que la surface sous la courbe puisse être calculée comme une somme de trapèzes.

 

 

Idée de la méthode

Lorsque l’intégrale exacte \( \large \int_a^b f(x)\,dx \) ne peut pas être trouvée, on peut diviser l’intervalle \( \large [a,b] \) en \( \large n \) sous-intervalles plus petits. Sur chaque sous-intervalle, la fonction est remplacée par une droite reliant les deux extrémités. L’aire sous cette droite est un trapèze, facile à calculer.

 

 

Formule de la méthode des trapèzes

Pour un intervalle divisé en \( \large n \) parties égales de largeur \( \large h = \frac{b-a}{n} \), on a :

 

$$ \large \int_a^b f(x)\,dx \approx \frac{h}{2} \left[f(x_0) + 2f(x_1) + 2f(x_2) + \ldots + 2f(x_{n-1}) + f(x_n)\right] $$

 

 

Démarche étape par étape

 

1. Diviser l’intervalle \( \large [a,b] \) en \( \large n \) parties égales.
2. Calculer \( \large h = \frac{b-a}{n} \).
3. Calculer les valeurs de la fonction \( \large f(x_0), f(x_1), \ldots, f(x_n) \).
4. Remplacer les valeurs dans la formule du trapèze.

 

 

Exemple

Nous allons calculer l’aire approchée sous la fonction \( \large f(x) = x^2 \) sur l’intervalle \( \large [0,2] \) en utilisant 4 trapèzes.

 

Ici \( \large a = 0 \), \( \large b = 2 \) et \( \large n = 4 \), donc \( \large h = \frac{2-0}{4} = 0{,}5 \).

 

Les valeurs de la fonction sont :

 

$$ \large f(0)=0, \quad f(0{,}5)=0{,}25, \quad f(1)=1, \quad f(1{,}5)=2{,}25, \quad f(2)=4 $$

 

La formule du trapèze donne :

 

$$ \large A \approx \frac{0{,}5}{2}\,[0 + 2(0{,}25 + 1 + 2{,}25) + 4] = 2{,}75 $$

 

L’intégrale exacte est \( \large \int_0^2 x^2\,dx = \frac{8}{3} \approx 2{,}67 \), donc la méthode fournit une bonne approximation.

 

 

 

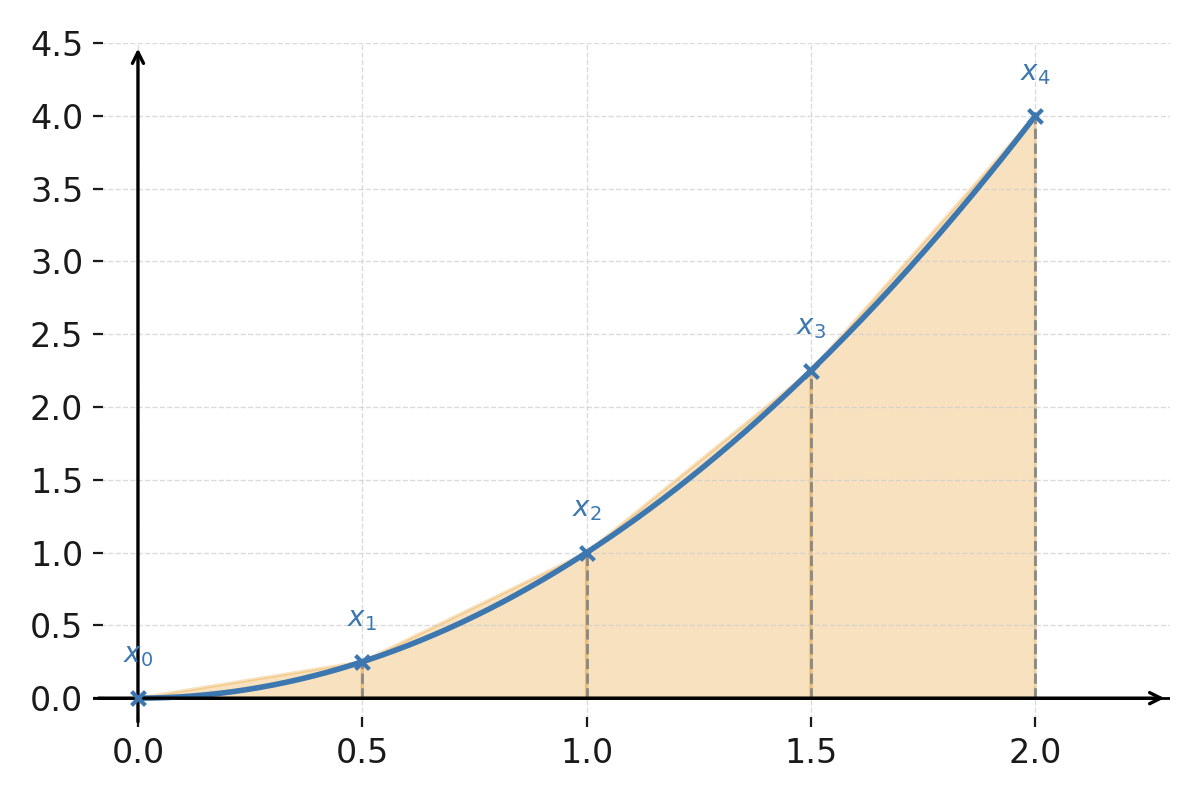
La fonction \( \large f(x) = x^2 \) sur l’intervalle \( \large [0,2] \).

Les quatre sous-intervalles sont marqués par des lignes verticales pointillées, et les trapèzes correspondants apparaissent entre la courbe et l’axe des x.

 

 

Remarques

La méthode des trapèzes est facile à mettre en œuvre et fournit souvent une bonne précision, mais elle peut sous-évaluer ou surestimer l’aire selon que la fonction est convexe ou concave. La précision peut être améliorée en utilisant plus de sous-intervalles ou en appliquant la règle de Simpson.