Différentiation numérique
Lorsqu’aucune formule analytique n’est disponible pour la fonction, la dérivée \( \large f'(x) \) peut être obtenue à l’aide de méthodes numériques. La différentiation numérique consiste à approximer la pente de la tangente à partir de points discrets plutôt que d’utiliser la valeur limite exacte.
Idée de la méthode
La dérivée en un point décrit la pente locale de la tangente à la fonction. Si les valeurs de la fonction sont connues en des points proches, on peut calculer une pente approximative entre eux. Cela se fait à l’aide de quotients de différences.
Différence avant, arrière et centrale
Il existe trois formules de base pour la différentiation numérique :
Différence avant :
$$ \large f'(x) \approx \frac{f(x+h) - f(x)}{h} $$
Différence arrière :
$$ \large f'(x) \approx \frac{f(x) - f(x-h)}{h} $$
Différence centrale :
$$ \large f'(x) \approx \frac{f(x+h) - f(x-h)}{2h} $$
La différence centrale offre généralement la meilleure précision, car elle prend en compte les points situés de part et d’autre de \( \large x \).
Exemple
Supposons que nous voulions calculer la dérivée de \( \large f(x) = x^2 \) au point \( \large x = 1 \) avec \( \large h = 0{,}1 \).
Les valeurs nécessaires de la fonction sont :
$$ \large f(1+h) = f(1{,}1) = 1{,}21, \quad f(1-h) = f(0{,}9) = 0{,}81 $$
En remplaçant dans les formules :
$$ \large f'_{\text{avant}}(1) = \frac{1{,}21 - 1}{0{,}1} = 2{,}1 $$
$$ \large f'_{\text{arrière}}(1) = \frac{1 - 0{,}81}{0{,}1} = 1{,}9 $$
$$ \large f'_{\text{centrale}}(1) = \frac{1{,}21 - 0{,}81}{0{,}2} = 2{,}0 $$
La valeur exacte de \( \large f'(x) = 2x \) est \( \large 2 \), donc la différence centrale donne le résultat le plus précis.
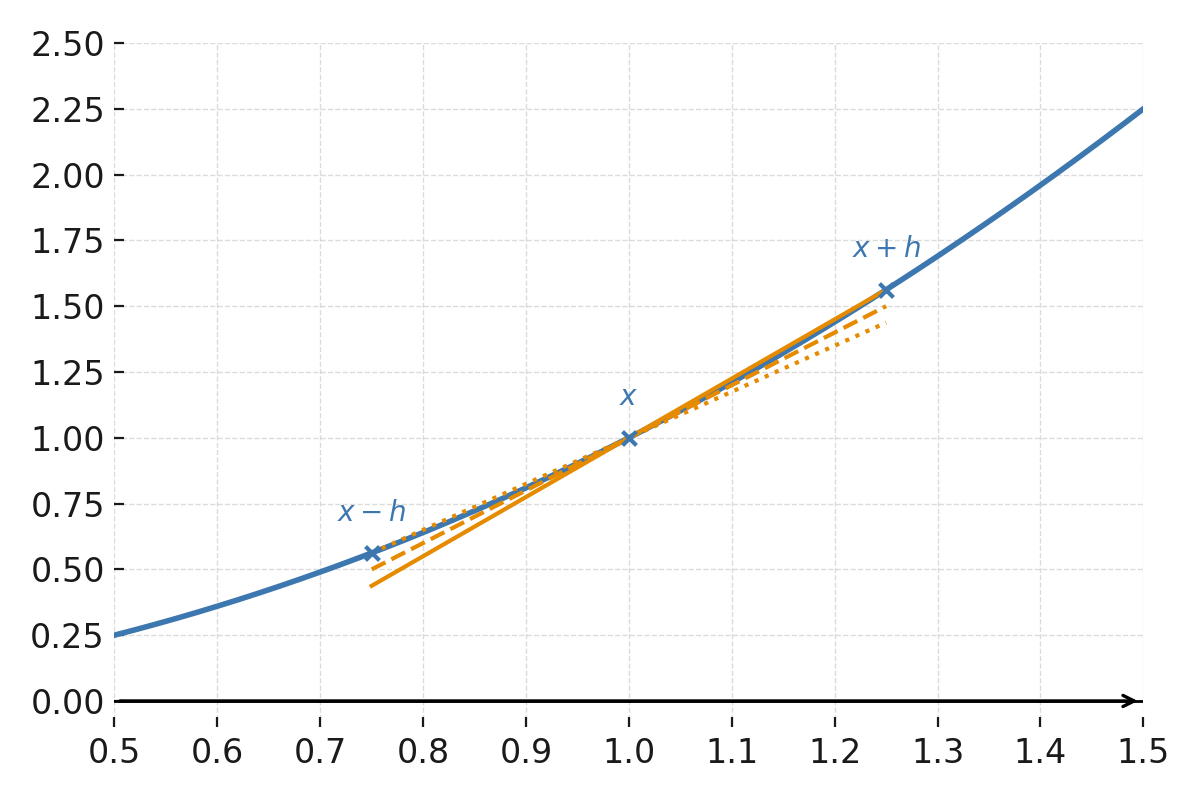
La fonction \( \large f(x) = x^2 \) autour du point \( \large x=1 \).
Les trois pentes (avant, arrière et centrale) illustrent la différence entre l’utilisation des points \( \large (x,f(x)) \), \( \large (x+h,f(x+h)) \) et \( \large (x-h,f(x-h)) \).
Remarques
La précision dépend de la taille de \( \large h \). Un \( \large h \) trop grand donne une mauvaise approximation, tandis qu’un \( \large h \) trop petit peut entraîner des erreurs d’arrondi. En pratique, on choisit \( \large h \) de manière à ce que le quotient de différence soit stable et fournisse une précision raisonnable.