Méthode de la sécante

La méthode de la sécantes est une méthode numérique pour trouver une racine d’une fonction, c’est-à-dire un point où \( \large f(x) = 0 \). Elle ressemble à la méthode de Newton-Raphson, mais au lieu d’utiliser la dérivée \( \large f'(x) \), la tangente est remplacée par une sécantes passant par deux points de la courbe.

 

 

Idée de la méthode

À chaque étape, les deux points les plus récents \( \large (x_{n-1}, f(x_{n-1})) \) et \( \large (x_n, f(x_n)) \) sont utilisés pour tracer une droite (sécantes). Le point d’intersection de cette droite avec l’axe des x est utilisé comme nouvelle estimation \( \large x_{n+1} \). Le processus est répété jusqu’à ce que deux estimations successives soient très proches.

 

 

Formule

 

$$ \large x_{n+1} = x_n - f(x_n) \cdot \frac{x_n - x_{n-1}}{f(x_n) - f(x_{n-1})} $$

 

 

Démarche étape par étape

 

1. Choisir deux valeurs initiales \( \large x_0 \) et \( \large x_1 \), où la fonction a des signes opposés.
2. Calculer \( \large f(x_0) \) et \( \large f(x_1) \).
3. Utiliser la formule pour trouver \( \large x_2 \).
4. Répéter le calcul de sorte que \( \large x_{n+1} \) soit calculé à partir des deux points les plus récents \( \large x_n \) et \( \large x_{n-1} \).
5. Arrêter lorsque \( \large |x_{n+1} - x_n| < \varepsilon \).

 

 

Exemple

Nous cherchons la racine de \( \large f(x) = x^3 - x - 2 \).

 

Choisir \( \large x_0 = 1 \) et \( \large x_1 = 2 \).

 

$$ \large f(1) = -2, \quad f(2) = 4 $$

 

$$ \large x_2 = 2 - 4 \cdot \frac{2 - 1}{4 - (-2)} $$

$$ \large x_2 = 2 - 4 \cdot \frac{1}{6} $$

$$ \large x_2 = 1{,}333 $$

 

Le nouveau point \( \large x_2 = 1{,}333 \) est utilisé avec \( \large x_1 = 2 \) pour calculer la valeur suivante :

 

$$ \large x_3 = 1{,}333 - f(1{,}333) \cdot \frac{1{,}333 - 2}{f(1{,}333) - f(2)} $$

 

Après quelques itérations, on obtient une racine \( \large x \approx 1{,}521 \), le même résultat qu’avec Newton-Raphson, mais sans connaître la dérivée de la fonction.

 

 

 

 

 

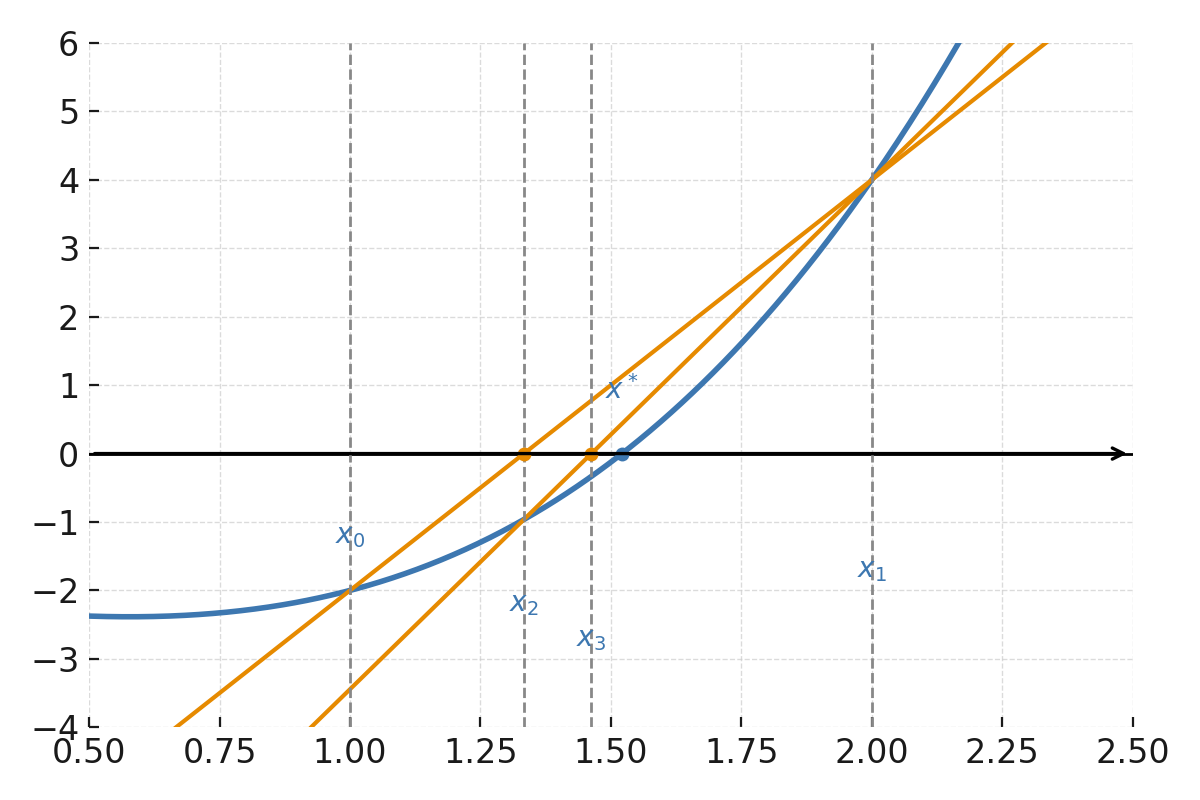
La fonction \( \large f(x) = x^3 - x - 2 \).

Les points \( \large (x_0, f(x_0)) \) et \( \large (x_1, f(x_1)) \) sont reliés par une sécantes qui coupe l’axe des x en \( \large x_2 \). Ensuite, une nouvelle sécantes est tracée entre \( \large (x_1, f(x_1)) \) et \( \large (x_2, f(x_2)) \), qui coupe l’axe encore plus près de la racine.

 

 

Remarques

La méthode de la sécantes converge plus rapidement que la méthode de bissection, mais plus lentement que Newton-Raphson. Cependant, elle constitue souvent un bon compromis, car elle ne nécessite pas le calcul de la dérivée de la fonction.