Méthode de dichotomie

La méthode de bissection est une technique numérique simple permettant de trouver une racine d’une fonction continue, c’est-à-dire un point où $ \large f(x) = 0 $.

La méthode repose sur le théorème des valeurs intermédiaires, qui indique que si $ \large f(a) $ et $ \large f(b) $ ont des signes opposés, alors il existe au moins une racine dans l’intervalle $ \large [a,b] $.

Idée de la méthode

L’intervalle est divisé répétément en deux moitiés. À chaque étape, on détermine dans quelle moitié la fonction change de signe. Cette moitié est choisie comme nouveau intervalle, et le processus est répété jusqu’à ce que la position de la racine soit connue avec la précision souhaitée.

Démarche étape par étape

Choisir un intervalle initial $ \large [a,b] $ où $ \large f(a) $ et $ \large f(b) $ ont des signes opposés.
Calculer le point milieu $ \large m = \frac{a + b}{2} $.
Évaluer $ \large f(m) $.
Si $ \large f(m) = 0 $ (ou très proche de 0), alors $ \large m $ est la racine.
Sinon, si $ \large f(a) $ et $ \large f(m) $ ont des signes opposés, poser $ \large b = m $; sinon poser $ \large a = m $.
Répéter les étapes 2–5 jusqu’à ce que la longueur de l’intervalle soit inférieure à la tolérance choisie $ \large \varepsilon $.

Exemple

Nous voulons trouver la racine de la fonction $ \large f(x) = x^3 - x - 2 $.

On observe que $ \large f(1) = -2 $ et $ \large f(2) = 4 $; la fonction change donc de signe dans l’intervalle $ \large [1,2] $.

$$ \large m_1 = \frac{1 + 2}{2} = 1{,}5 $$

$$ \large f(1{,}5) = (1{,}5)^3 - 1{,}5 - 2 $$

$$ \large f(1{,}5) = -0{,}125 $$

Comme $ \large f(1{,}5) $ et $ \large f(2) $ ont des signes opposés, on choisit un nouvel intervalle $ \large [1{,}5, 2] $.

$$ \large m_2 = \frac{1{,}5 + 2}{2} = 1{,}75 $$

$$ \large f(1{,}75) = (1{,}75)^3 - 1{,}75 - 2 $$

$$ \large f(1{,}75) = 1{,}609 - 3{,}75 $$

$$ \large f(1{,}75) = -0{,}109 $$

Le processus est répété jusqu’à ce que $ \large a $ et $ \large b $ soient suffisamment proches pour que la racine puisse être lue comme $ \large x \approx 1{,}521 $.

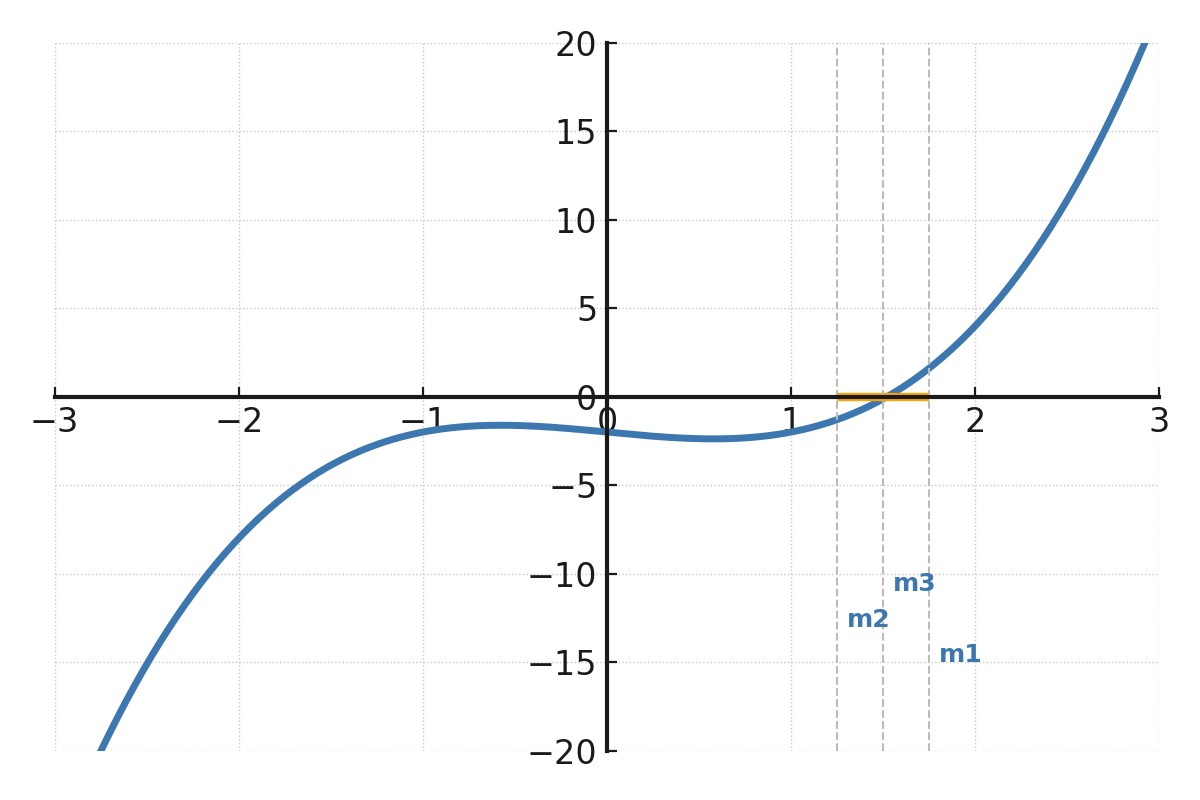
Méthode de bissection

La fonction $ \large f(x) = x^3 - x - 2 $, où l’intervalle $ \large [1,2] $ est marqué par une ligne sur l’axe des x.

Les points milieux $ \large m_1, m_2, m_3 $ apparaissent comme des lignes verticales qui se rapprochent progressivement de la position de la racine, là où la courbe coupe l’axe des x.

Remarque

La méthode de bissection est très robuste, car elle converge toujours si la fonction est continue et change de signe. L’inconvénient est qu’elle converge lentement par rapport à des méthodes plus avancées comme Newton-Raphson.