Règle de Simpson

La règle de Simpson est une amélioration de la méthode des trapèzes pour calculer numériquement une intégrale définie. Alors que la méthode des trapèzes remplace la fonction par des lignes droites, la règle de Simpson utilise des paraboles (polynômes du second degré) pour approcher la courbe. Cela permet d’obtenir une bien meilleure précision, même avec peu de sous-intervalles.

 

 

Idée de la méthode

Supposons que l’on veuille calculer l’aire sous la fonction \( \large f(x) \) entre \( \large a \) et \( \large b \). L’intervalle est divisé en un nombre pair de sous-intervalles (par exemple \( \large n = 4 \)). Sur chaque paire de sous-intervalles, on trace une parabole passant par les trois points \( \large (x_{2i}, f(x_{2i})) \), \( \large (x_{2i+1}, f(x_{2i+1})) \) et \( \large (x_{2i+2}, f(x_{2i+2})) \). La somme des aires sous ces paraboles donne une approximation de l’intégrale totale.

 

 

Formule de la règle de Simpson

Si \( \large n \) est un nombre pair et que la largeur des sous-intervalles est \( \large h = \frac{b-a}{n} \), alors :

 

$$ \large \int_a^b f(x)\,dx \approx \frac{h}{3}\,[f(x_0) + 4f(x_1) + 2f(x_2) + 4f(x_3) + \ldots + 4f(x_{n-1}) + f(x_n)] $$

 

Démarche étape par étape

 

1. Diviser l’intervalle \( \large [a,b] \) en un nombre pair de sous-intervalles \( \large n \).
2. Calculer \( \large h = \frac{b-a}{n} \).
3. Calculer les valeurs de la fonction \( \large f(x_0), f(x_1), \ldots, f(x_n) \).
4. Remplacer les valeurs dans la formule de Simpson.

 

 

Exemple

Nous calculons l’aire approchée sous \( \large f(x) = x^2 \) sur l’intervalle \( \large [0,2] \) avec \( \large n = 4 \).

 

Ici, \( \large h = \frac{2-0}{4} = 0{,}5 \).

 

Les valeurs de la fonction sont :

 

$$ \large f(0)=0, \quad f(0{,}5)=0{,}25, \quad f(1)=1, \quad f(1{,}5)=2{,}25, \quad f(2)=4 $$

 

En remplaçant dans la formule de Simpson, on obtient :

 

$$ \large A \approx \frac{0{,}5}{3}\,[0 + 4(0{,}25) + 2(1) + 4(2{,}25) + 4] = 2{,}67 $$

 

Cela correspond exactement à l’intégrale exacte :

 

$$ \large \int_0^2 x^2\,dx = \frac{8}{3} = 2{,}67 $$

 

 

 

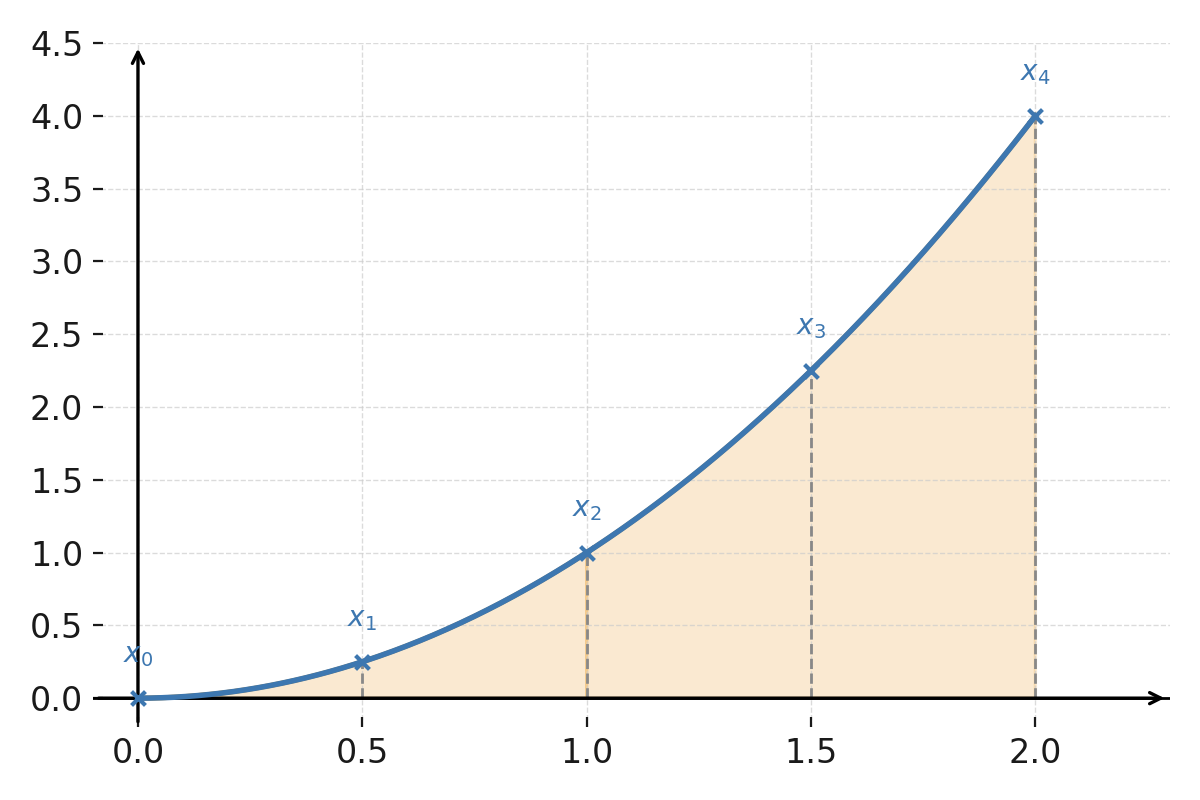
La fonction \( \large f(x)=x^2 \).

Sur chaque paire de sous-intervalles, une parabole approxime la fonction. Les limites \( \large x_0, x_1, x_2, x_3, x_4 \) sont marquées par des lignes grises pointillées.

 

 

Remarques

La règle de Simpson offre une bien meilleure précision que la méthode des trapèzes, car elle tient compte de la courbure de la fonction. Cependant, elle ne peut être appliquée que si le nombre de sous-intervalles \( \large n \) est pair. Lorsqu’elle est combinée sur plusieurs paraboles, on parle de la règle de Simpson composée.