Méthode de Newton-Raphson

La méthode de Newton-Raphson est une technique numérique rapide pour trouver les zéros d’une fonction, c’est-à-dire les points où $ \large f(x) = 0 $. Elle utilise à la fois la valeur de la fonction et sa dérivée pour améliorer l’estimation de la position de la racine.

Idée de la méthode

Le point de départ est une estimation initiale $ \large x_0 $. Au point $ \large (x_0, f(x_0)) $, on trace la tangente à la courbe. Le point d’intersection de cette tangente avec l’axe des x est utilisé comme nouvelle estimation $ \large x_1 $. Le processus est répété jusqu’à ce que la différence entre deux estimations successives soit inférieure à une tolérance choisie $ \large \varepsilon $.

Formule

$$ \large x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} $$

Démarche étape par étape

Choisir un point de départ $ \large x_0 $.
Calculer $ \large f(x_0) $ et $ \large f'(x_0) $.
Utiliser la formule pour trouver $ \large x_1 $.
Répéter jusqu’à ce que $ \large |x_{n+1} - x_n| < \varepsilon $.

Exemple

Nous voulons trouver la racine de $ \large f(x) = x^3 - x - 2 $, que nous avons déjà résolue avec la méthode de bissection.

La dérivée est $ \large f'(x) = 3x^2 - 1 $.

Nous choisissons une estimation initiale $ \large x_0 = 1{,}5 $.

$$ \large f(1{,}5) = (1{,}5)^3 - 1{,}5 - 2$$

$$ \large f(1{,}5) = -0{,}125 $$

$$ \large f'(1{,}5) = 3(1{,}5)^2 - 1 $$

$$ \large f'(1{,}5) = 5{,}75 $$

$$ \large x_1 = 1{,}5 - \frac{-0{,}125}{5{,}75} $$

$$ \large x_1 = 1{,}5217 $$

Après quelques itérations, la méthode converge rapidement vers la racine $ \large x \approx 1{,}521 $.

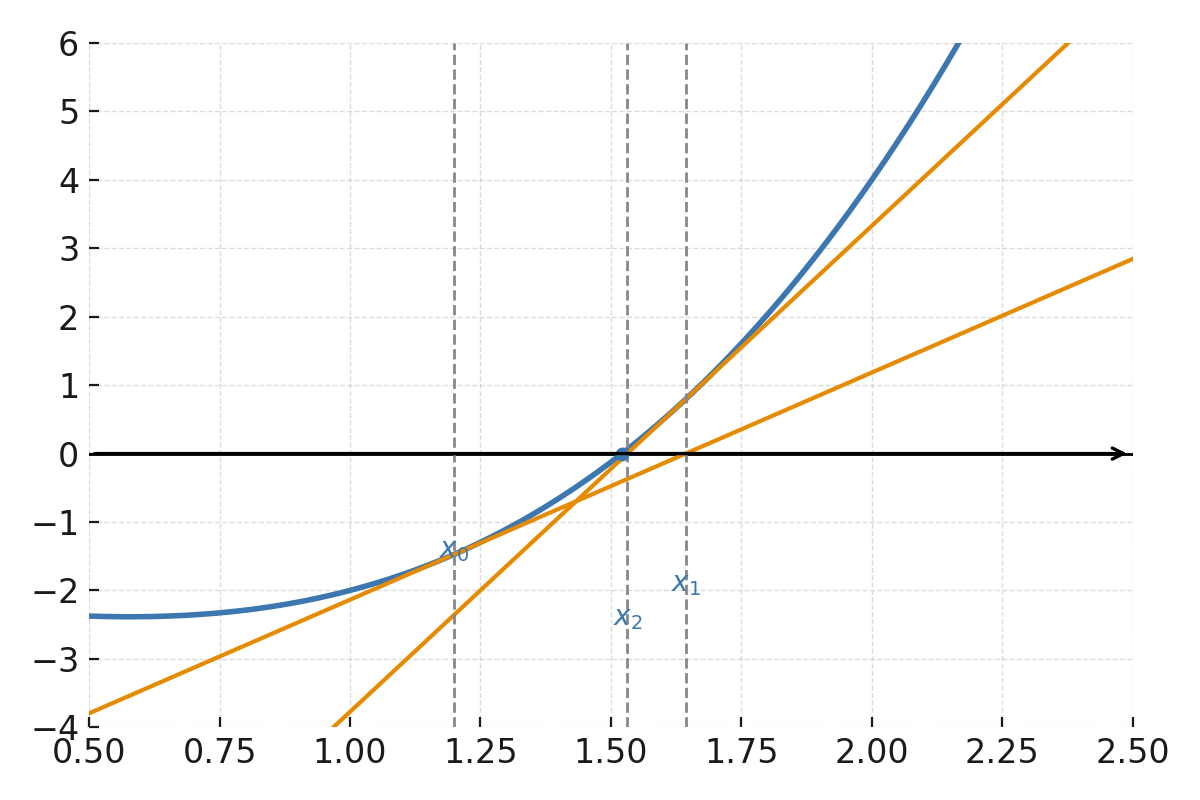
Méthode de Newton-Raphson

La fonction $ \large f(x) = x^3 - x - 2 $. L’estimation initiale $ \large x_0 $ est marquée sur l’axe des x, et la tangente en $ \large x_0 $ est tracée comme une ligne qui coupe l’axe des x en $ \large x_1 $. Ensuite, la tangente en $ \large x_1 $ est montrée, coupant encore plus près de la racine. La figure illustre l’amélioration itérative.

Remarques

La méthode de Newton-Raphson converge beaucoup plus rapidement que la méthode de bissection, mais elle nécessite que la dérivée $ \large f'(x) $ puisse être calculée et que l’estimation initiale soit proche de la racine réelle. Si la tangente est presque horizontale (c’est-à-dire $ \large f'(x) \approx 0 $), la méthode peut échouer ou dépasser la racine.