Méthodes avancées

Une fois que l’on a appris les règles de base du calcul différentiel, un nouveau monde de possibilités s’ouvre. De nombreuses fonctions ne peuvent pas être écrites directement sous la forme \( \large y = f(x) \), mais elles peuvent tout de même être différenciées à l’aide de méthodes étendues. Les trois techniques les plus importantes sont la différentiation implicite, la différentiation paramétrique et la dérivée des fonctions inverses.

 

 

Différentiation implicite

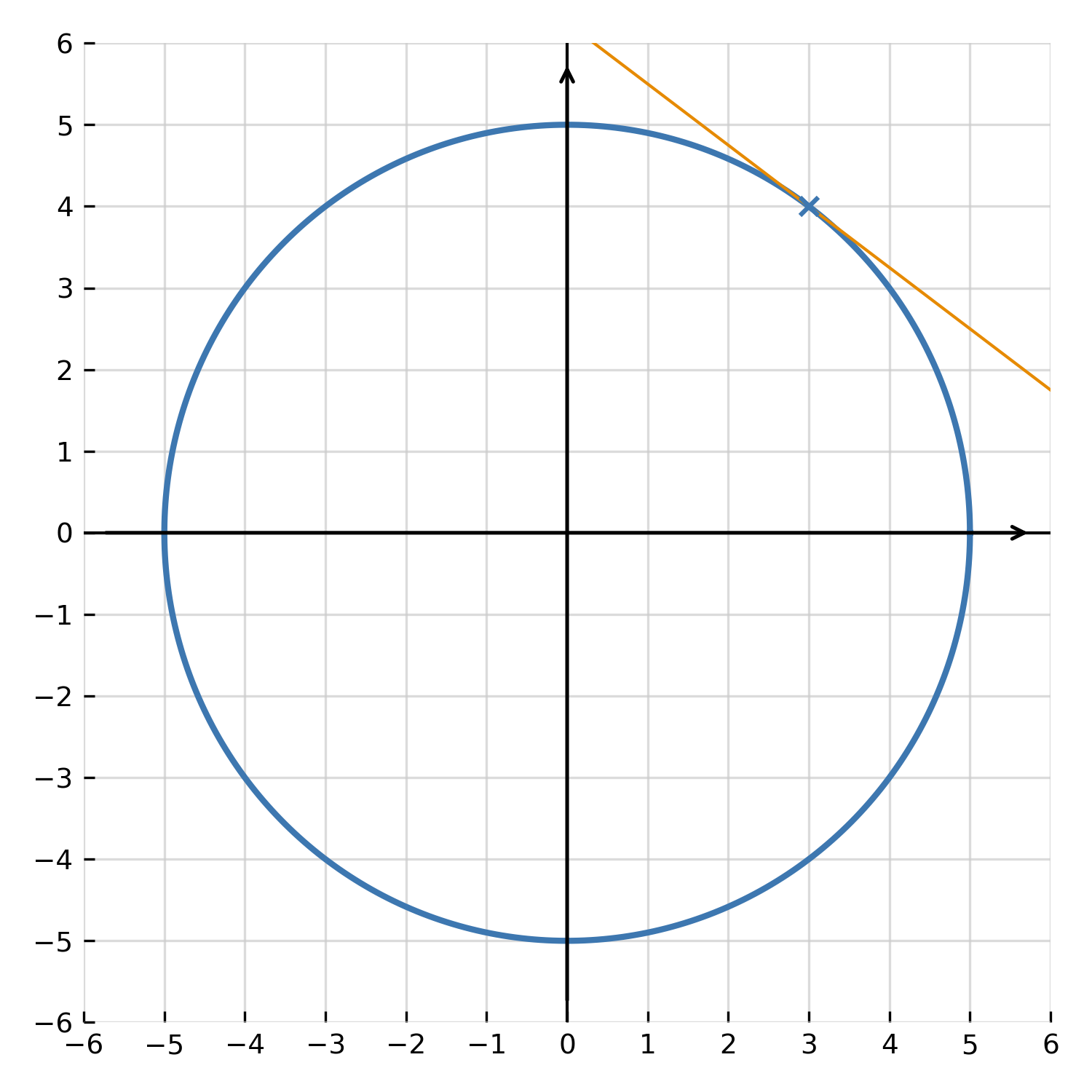
Certaines fonctions sont définies par une équation où \( \large x \) et \( \large y \) apparaissent ensemble, par exemple \( \large x^2 + y^2 = 25 \). Il est impossible d’isoler directement \( \large y \), mais on peut trouver \( \large \frac{dy}{dx} \) en différenciant les deux côtés par rapport à \( \large x \), en se souvenant que \( \large y \) dépend également de \( \large x \).

 

Exemple :

 

Différencier \( \large x^2 + y^2 = 25 \) par rapport à \( \large x \) :

 

$$ \large 2x + 2y \cdot \frac{dy}{dx} = 0 $$

 

Résoudre pour \( \large \frac{dy}{dx} \) :

 

$$ \large \frac{dy}{dx} = -\frac{x}{y} $$

 

C’est la pente de la tangente au cercle \( \large x^2 + y^2 = 25 \) en tout point. La différentiation implicite est particulièrement utile pour les courbes qui ne peuvent pas être décrites comme des fonctions au sens traditionnel, telles que les cercles, les ellipses et les hyperboles.

 

Règle de la chaîne en pratique

La règle de la chaîne est utilisée lorsqu’une fonction est composée d’une autre fonction. Elle est essentielle à toutes les méthodes étendues. On peut la voir comme « un changement qui en influence un autre ».

 

Exemple :

 

Si \( \large y = \sin(3x^2) \), la fonction comporte deux couches : \( \large \sin(u) \) où \( \large u = 3x^2 \). On trouve la dérivée en multipliant les deux taux de variation :

 

$$ \large \frac{dy}{dx} = \cos(3x^2) \cdot 6x = 6x \cos(3x^2) $$

 

La règle de la chaîne peut aussi être appliquée plusieurs fois, par exemple lorsque la fonction est composée de trois ou plusieurs couches. Elle devient donc un outil indispensable dans tous les calculs avancés.

 

 

Fonctions paramétriques

Parfois, \( \large x \) et \( \large y \) sont toutes deux données comme fonctions d’une troisième variable, souvent appelée \( \large t \) (le paramètre). Cela se produit, par exemple, en cinématique, lorsqu’une particule se déplace dans l’espace et que sa position est connue en fonction du temps.

 

Si \( \large x = x(t) \) et \( \large y = y(t) \), on peut trouver \( \large \frac{dy}{dx} \) en combinant les deux dérivées par rapport à \( \large t \) :

 

$$ \large \frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}} $$

 

Exemple :

 

Si \( \large x = t^2 \) et \( \large y = 3t + 1 \), alors :

$$ \large \frac{dx}{dt} = 2t \qquad \text{et} \qquad \frac{dy}{dt} = 3 $$

 

Ainsi :

$$ \large \frac{dy}{dx} = \frac{3}{2t} $$

 

Cette expression montre la pente de la courbe au point correspondant au paramètre \( \large t \).

 

 

Fonctions inverses

Si une fonction possède une inverse, on peut également trouver la dérivée de cette inverse sans la déterminer explicitement. Soit \( \large y = f(x) \) une fonction différentiable ayant pour inverse \( \large x = f^{-1}(y) \). On a :

 

$$ \large \frac{dy}{dx} = f'(x) \quad \Rightarrow \quad \frac{dx}{dy} = \frac{1}{f'(x)} $$

 

Autrement dit, la dérivée de la fonction inverse est la valeur réciproque de la dérivée de la fonction originale.

 

Exemple :

 

Si \( \large f(x) = e^x \), alors \( \large f^{-1}(x) = \ln(x) \). Puisque \( \large f'(x) = e^x \), on obtient :

 

$$ \large (\ln x)' = \frac{1}{e^x} = \frac{1}{x} $$

 

Cela correspond à la dérivée bien connue du logarithme et illustre le principe en pratique.

 

 

Méthodes combinées

On rencontre souvent des fonctions où plusieurs de ces techniques doivent être utilisées ensemble — par exemple, une équation implicite comportant un paramètre, ou une fonction composée qu’il faut inverser. Le calculateur expérimenté apprend à combiner naturellement les règles :

 

$$ \large \frac{dy}{dx} = \frac{dy}{dt} \cdot \frac{dt}{dx} $$

 

Il s’agit en réalité d’une version étendue de la règle de la chaîne, qui permet de passer d’une variable à une autre selon les besoins.

 

 

Résumé

Les méthodes étendues permettent de différencier des fonctions qui ne peuvent pas être écrites sous une forme simple. La différentiation implicite est utilisée pour les relations entre \( \large x \) et \( \large y \), la différentiation paramétrique s’applique lorsque les deux dépendent d’un paramètre, et la règle des fonctions inverses permet de trouver les dérivées des logarithmes et des fonctions trigonométriques inverses. Ces outils étendent la portée du calcul différentiel et constituent la base de sujets plus avancés en analyse.