Applications du calcul différentiel

Le calcul différentiel n’est pas seulement utilisé pour calculer des pentes. Il offre également une compréhension plus profonde du comportement des fonctions. En étudiant la dérivée, on peut déterminer où une fonction croît ou décroît, trouver ses maximums et minimums, et analyser sa forme graphique. La méthode est appliquée dans des domaines aussi variés que la physique, l’économie, la biologie et la technique.

Monotonie : où la fonction croît et décroît

La fonction dérivée $ \large f'(x) $ indique si $ \large f(x) $ est croissante ou décroissante sur un intervalle donné :

Si $ \large f'(x) > 0 $, la fonction est croissante.
Si $ \large f'(x) < 0 $, la fonction est décroissante.
Si $ \large f'(x) = 0 $, la fonction possède un point stationnaire.

Un point stationnaire est un endroit où la pente de la tangente est nulle. Il peut s’agir d’un maximum local, d’un minimum local ou d’un point d’inflexion.

Exemple : analyse d’une fonction

Analysons la fonction $ \large f(x) = x^3 - 3x^2 + 2 $.

On commence par calculer la dérivée :

$$ \large f'(x) = 3x^2 - 6x = 3x(x - 2) $$

La dérivée est nulle pour $ \large x = 0 $ et $ \large x = 2 $. Examinons le signe de $ \large f'(x) $ dans les intervalles :

Pour $ \large x < 0 $ : $ \large f'(x) > 0 $ → croissante
Pour $ \large 0 < x < 2 $ : $ \large f'(x) < 0 $ → décroissante
Pour $ \large x > 2 $ : $ \large f'(x) > 0 $ → croissante

La fonction possède donc un maximum local en $ \large x = 0 $ et un minimum local en $ \large x = 2 $. Cette méthode est appelée tableau de signes et sert à déterminer les intervalles de croissance et de décroissance d’une fonction.

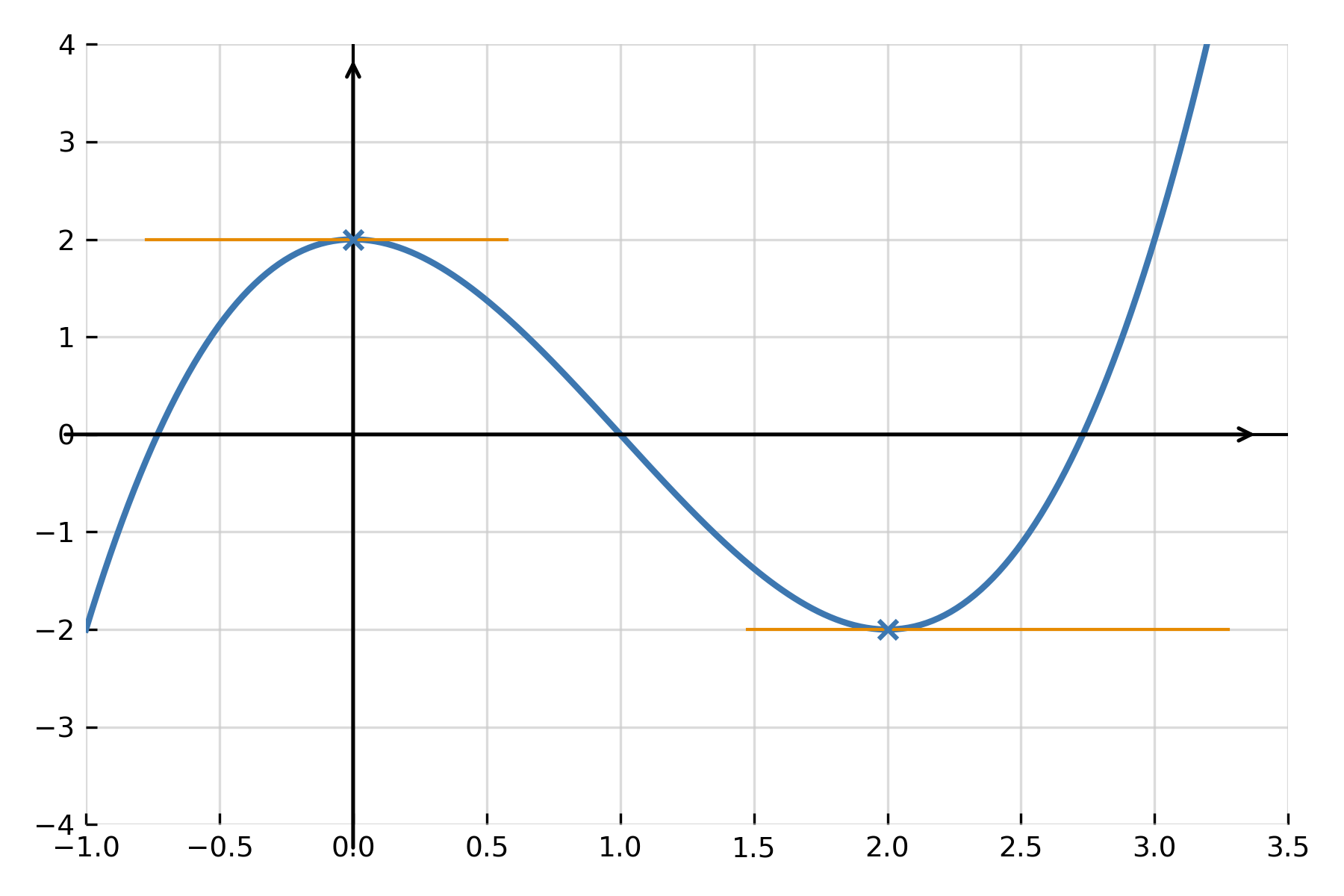
Extrémum

Extréma, maximum et minimum

Un extrémum est un point où la fonction passe de croissante à décroissante (maximum) ou de décroissante à croissante (minimum). Pour en déterminer le type, on examine le signe de $ \large f'(x) $ autour du point — ou on utilise la seconde dérivée.

Le test de la seconde dérivée stipule :

Si $ \large f'(x_0) = 0 $ et $ \large f''(x_0) > 0 $, la fonction possède un minimum local en $ \large x_0 $.
Si $ \large f'(x_0) = 0 $ et $ \large f''(x_0) < 0 $, la fonction possède un maximum local en $ \large x_0 $.

Exemple : pour $ \large f(x) = x^3 - 3x^2 + 2 $, on a $ \large f''(x) = 6x - 6 $. Ici $ \large f''(0) = -6 < 0 $ (maximum) et $ \large f''(2) = 6 > 0 $ (minimum).

Points d’inflexion

Un point d’inflexion est un endroit où la courbure du graphe change de signe. Cela signifie que la courbe passe de « concave vers le haut » à « concave vers le bas » ou inversement. Un point d’inflexion se trouve lorsque $ \large f''(x) = 0 $ et que le signe change.

Exemple : pour $ \large f(x) = x^3 - 3x^2 + 2 $, on a $ \large f''(x) = 6x - 6 $, qui s’annule pour $ \large x = 1 $. Comme le signe change, la fonction possède un point d’inflexion en $ \large x = 1 $.

Optimisation

Le calcul différentiel est souvent utilisé pour résoudre des problèmes d’optimisation — c’est-à-dire pour trouver la plus grande ou la plus petite valeur d’une fonction sous certaines conditions. Cela peut consister, par exemple, à maximiser une aire, minimiser un coût ou trouver le chemin le plus rapide.

Procédure étape par étape :

Écrire la fonction à optimiser.
Calculer sa dérivée $ \large f'(x) $.
Trouver les points où $ \large f'(x) = 0 $ (points stationnaires).
Utiliser le signe ou la seconde dérivée pour déterminer s’il s’agit d’un maximum ou d’un minimum.

Exemple – optimisation

Un rectangle possède une aire qui dépend de sa longueur $ \large x $ :

$$ \large A(x) = x(12 - 2x) = 12x - 2x^2 $$

Pour trouver l’aire maximale, on dérive la fonction :

$$ \large A'(x) = 12 - 4x $$

On pose $ \large A'(x) = 0 $ → $ \large 12 - 4x = 0 \Rightarrow x = 3 $.

La seconde dérivée $ \large A''(x) = -4 $ est négative, il s’agit donc d’un maximum. Le rectangle a donc une aire maximale lorsque la longueur vaut $ \large 3 $ et la largeur $ \large 12 - 2x = 6 $.

Esquisse graphique et interprétation

En combinant les informations de $ \large f'(x) $ et $ \large f''(x) $, on peut tracer une courbe précise sans calculatrice :

$ \large f'(x) $ indique où la courbe monte ou descend.
$ \large f''(x) $ indique si la courbe est concave vers le haut ou vers le bas.
$ \large f'(x) = 0 $ donne les sommets et les creux.
$ \large f''(x) = 0 $ donne les points d’inflexion.

Ceci est appelé une analyse graphique complète et constitue la base à la fois de la compréhension théorique et des applications pratiques des fonctions en sciences et en technologie.

Résumé

La dérivée permet d’analyser et de prédire le comportement d’une fonction. Avec le calcul différentiel, on peut trouver les maximums et minimums, déterminer les intervalles de croissance ou de décroissance, étudier la forme du graphe et résoudre des problèmes d’optimisation. Cela en fait l’un des outils les plus utiles de toute la mathématique.