La fonction dérivée

La fonction dérivée indique la vitesse à laquelle une autre fonction varie. Si $ \large f(x) $ représente une grandeur, la dérivée $ \large f'(x) $ montre de combien cette grandeur change lorsque $ \large x $ varie légèrement. Ainsi, le calcul différentiel devient un outil précis pour mesurer le changement.

De la sécante à la tangente

Pour comprendre ce que signifie « dériver », on commence par la pente d’une sécante. Une sécante est la droite reliant deux points du graphe de $ \large f(x) $. La pente de la sécante indique de combien la fonction augmente ou diminue en moyenne entre ces deux points.

$$ \large a_{\text{sécante}} = \frac{f(x+h) - f(x)}{h} $$

Si l’on choisit les points de plus en plus proches, de sorte que $ \large h $ devienne très petit, la sécante se rapproche d’une droite qui touche le graphe en un seul point — la tangente. La pente de cette tangente est appelée le taux de variation instantané. C’est précisément la valeur donnée par la fonction dérivée.

Tangente et sécante dans la fonction dérivée

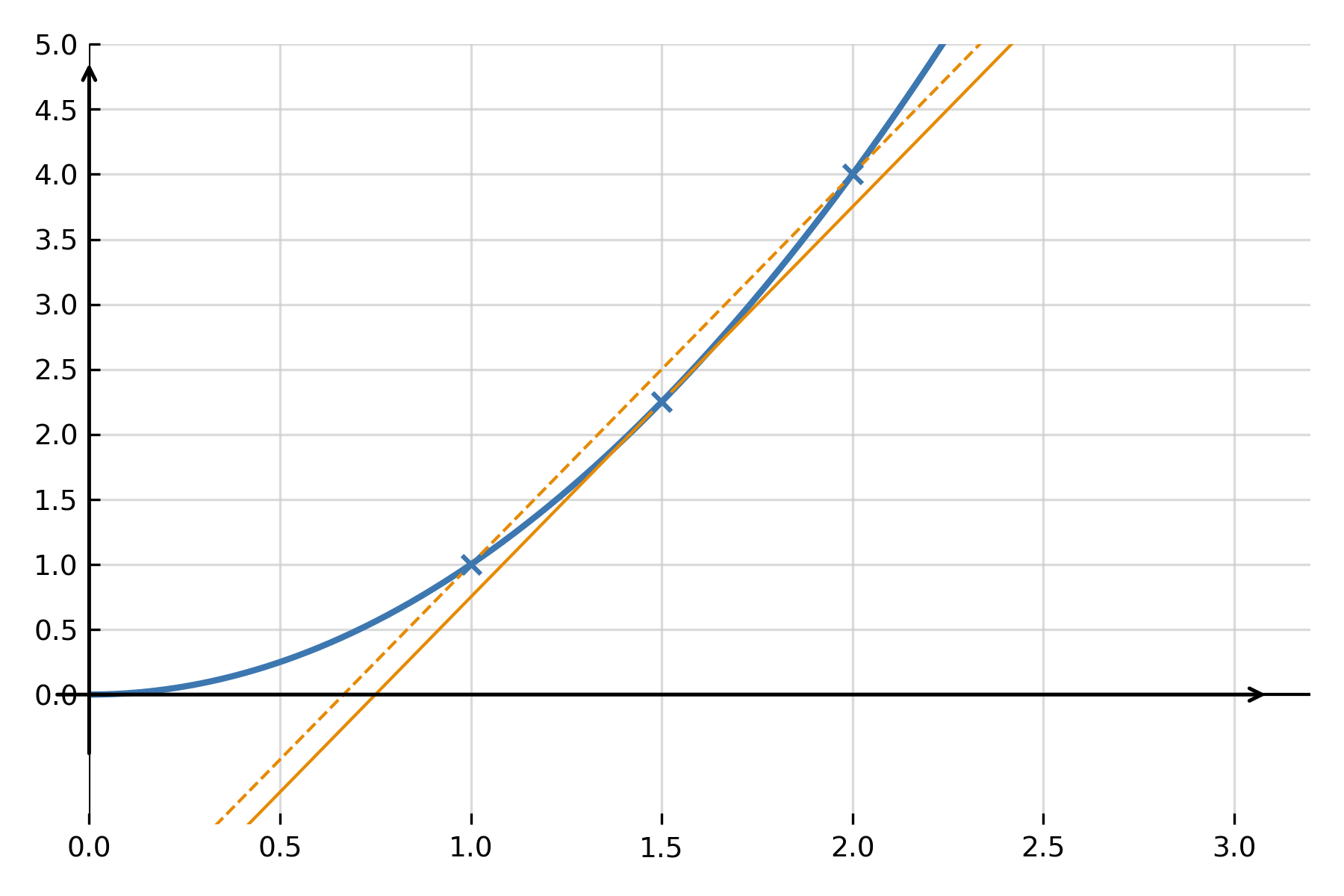
Définition par la limite

La définition précise de la fonction dérivée est :

$$ \large f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} $$

Ici, la fraction mesure de combien $ \large f(x) $ varie lorsque $ \large x $ change d’une petite quantité $ \large h $. Lorsque $ \large h $ tend vers zéro, on obtient la variation en ce point précis — la pente de la tangente. La limite n’existe que si la fonction est suffisamment lisse à ce point, c’est-à-dire sans sauts, pointes ou cassures.

Notation et lecture

Il existe plusieurs façons d’écrire la dérivée :

$$ \large f'(x) \quad \text{ou} \quad \frac{dy}{dx} \quad \text{ou} \quad Df(x) $$

Toutes signifient la même chose : combien $ \large y $ change lorsque $ \large x $ change. En physique, par exemple, $ \large \frac{dy}{dt} $ se lit « variation de la distance sur variation du temps », c’est-à-dire la vitesse.

Compréhension graphique

La fonction dérivée donne une nouvelle fonction qui, en chaque point, indique la pente du graphe de $ \large f(x) $. Là où le graphe monte, la dérivée est positive ; là où il descend, elle est négative ; et là où le graphe a une tangente horizontale, la dérivée est nulle.

Un point où $ \large f'(x) = 0 $ est appelé un point stationnaire. Ces points jouent un rôle important plus tard pour déterminer les maxima et minima des fonctions.

Interprétation physique

Dans de nombreux contextes, la dérivée représente une grandeur physique. Si $ \large f(x) $ décrit une position en fonction du temps, alors $ \large f'(x) $ est la vitesse — la rapidité du mouvement. En dérivant une fois de plus, on obtient l’accélération $ \large f''(x) $, qui montre la rapidité du changement de la vitesse elle-même.

Exemples

1. Exemple – fonction quadratique

Pour $ \large f(x) = x^2 $, on peut calculer la dérivée directement à partir de la définition :

$$ \large f'(x) = \lim_{h \to 0} \frac{(x+h)^2 - x^2}{h} = \lim_{h \to 0} \frac{2xh + h^2}{h} = 2x $$

La fonction dérivée est $ \large f'(x) = 2x $. La pente dépend donc de l’endroit sur le graphe. En $ \large x = 3 $, la pente est $ \large f'(3) = 6 $.

2. Exemple – fonction linéaire

Pour $ \large f(x) = 5x + 2 $, le graphe est déjà une droite. Sa pente est constante, donc la dérivée est :

$$ \large f'(x) = 5 $$

Ici, la fonction augmente toujours de 5 unités lorsque $ \large x $ augmente de 1. Cela montre que le calcul différentiel généralise la notion de pente connue des droites à toutes les fonctions lisses.

3. Exemple – interprétation physique

Si $ \large s(t) = t^2 $ décrit la distance parcourue par une voiture en mètres en fonction du temps $ \large t $ en secondes, alors la vitesse est $ \large v(t) = s'(t) = 2t $. Après 4 secondes, la voiture roule à $ \large v(4) = 8 $ m/s. La dérivée fournit ici une mesure directe de la vitesse du mouvement.

Règles simples

Pour trouver les dérivées des fonctions courantes, quelques règles simples s’appliquent :

$$ \large (k)' = 0 \qquad (x^n)' = n \cdot x^{n-1} \qquad (k \cdot f(x))' = k \cdot f'(x) $$

Ces règles constituent la base des règles générales de dérivation présentées dans la section suivante. Grâce à elles, on peut dériver même des fonctions assez complexes sans revenir à la définition par la limite.

Résumé

La fonction dérivée exprime la rapidité avec laquelle une fonction varie en chaque point. Elle peut être comprise comme la pente de la tangente, comme une mesure du taux de variation ou comme un outil mathématique pour décrire le mouvement et la croissance. Elle joue un rôle central dans presque tous les domaines des mathématiques, de la physique et de l’économie.