Linéarisation et approximation
Le calcul différentiel permet de comprendre et d’approcher les fonctions localement. Lorsqu’une fonction est lisse et différentiable, on peut la remplacer, dans une petite région autour d’un point, par une droite – c’est-à-dire la tangente. Cette méthode s’appelle linéarisation et sert à trouver des approximations rapides lorsque les calculs exacts sont difficiles ou inutiles.
L’idée de la linéarisation
Au voisinage d’un point \( \large x_0 \), une fonction différentiable \( \large f(x) \) se comporte presque comme sa tangente. Si l’on connaît la fonction et sa dérivée en ce point, on peut décrire tout son comportement local à l’aide d’une fonction linéaire, facile à manipuler.
L’approximation linéaire (l’équation de la tangente) a la forme :
$$ \large f(x) \approx f(x_0) + f'(x_0) \cdot (x - x_0) $$
Cette expression indique que la valeur de la fonction en un point proche de \( \large x_0 \) peut être approximée par la valeur en \( \large x_0 \) augmentée du changement donné par la pente \( \large f'(x_0) \). Plus \( \large x \) est proche de \( \large x_0 \), meilleure est l’approximation.
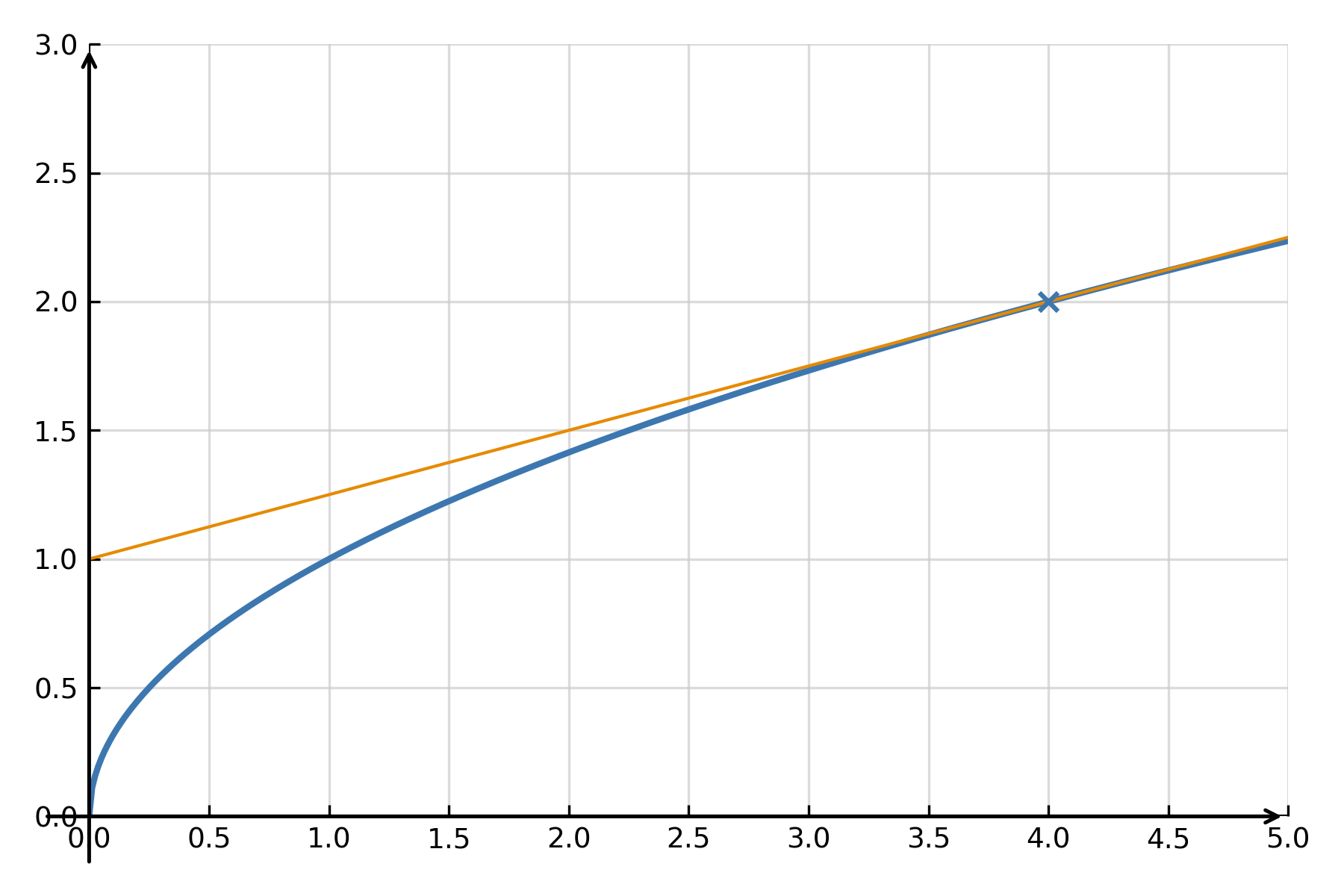
Compréhension graphique
La tangente « touche » la courbe de \( \large f(x) \) en un seul point et suit sa direction à cet endroit. Pour de petites variations de \( \large x \), la fonction et la tangente sont presque confondues. La linéarisation consiste donc à remplacer une courbe par sa droite locale. Cela simplifie considérablement les calculs sans perdre de précision dans cette zone.
Exemple 1 : Linéarisation d’une fonction quadratique
Trouver l’approximation linéaire de \( \large f(x) = x^2 \) autour du point \( \large x_0 = 2 \).
On a \( \large f(2) = 4 \) et \( \large f'(x) = 2x \), donc \( \large f'(2) = 4 \). Ainsi :
$$ \large f(x) \approx 4 + 4(x - 2) = 4x - 4 $$
Lorsque \( \large x \) est proche de 2, \( \large 4x - 4 \) est une bonne approximation de \( \large x^2 \). Par exemple, \( \large f(2.1) \approx 4.4 \), tandis que la valeur exacte est \( \large 2.1^2 = 4.41 \).
Exemple 2 : Approximation d’une racine carrée
La linéarisation peut être utilisée pour approximer des racines carrées sans calculatrice. Par exemple, \( \large \sqrt{4.1} \) peut être trouvée en linéarisant la fonction \( \large f(x) = \sqrt{x} \) autour de \( \large x_0 = 4 \).
Ici, \( \large f(4) = 2 \) et \( \large f'(x) = \frac{1}{2\sqrt{x}} \), donc \( \large f'(4) = \frac{1}{4} \).
$$ \large f(x) \approx 2 + \frac{1}{4}(x - 4) $$
Pour \( \large x = 4.1 \) : \( \large f(4.1) \approx 2 + \frac{1}{4} \cdot 0.1 = 2.025 \), tandis que la valeur exacte est \( \large 2.0248 \). L’approximation tangente donne donc un résultat presque exact.
Erreur et précision
Plus \( \large x \) est proche de \( \large x_0 \), meilleure est l’approximation. Si l’on s’éloigne, la droite tangente commence à s’écarter de la courbe originale, car les termes d’ordre supérieur (courbure) deviennent significatifs. Cela peut être corrigé en ajoutant davantage de termes dans un développement de Taylor.
Au premier ordre, la linéarisation correspond à la première partie de la série de Taylor :
$$ \large f(x) = f(x_0) + f'(x_0)(x - x_0) + \frac{f''(x_0)}{2!}(x - x_0)^2 + \dots $$
En ne prenant que le premier terme après \( \large f(x_0) \), on obtient précisément l’approximation tangente. C’est pourquoi la méthode est aussi appelée approximation de Taylor du premier ordre.
Exemple 3 : Interprétation physique
En physique, la linéarisation est utilisée pour décrire les mouvements ou les processus sur de courts intervalles de temps. Si \( \large s(t) \) décrit une position, l’approximation linéaire
$$ \large s(t) \approx s(t_0) + v(t_0) \cdot (t - t_0) $$
peut être interprétée comme : « la nouvelle position est l’ancienne plus la vitesse multipliée par le temps ». Ici, la vitesse \( \large v(t_0) = s'(t_0) \) joue exactement le même rôle que la pente de la tangente en mathématiques.
Résumé
La linéarisation permet de remplacer une fonction par un modèle linéaire simple autour d’un point donné. La droite tangente agit comme une approximation locale rapide et souvent suffisamment précise. La méthode constitue la base de nombreux procédés numériques et du développement de Taylor, qui généralise l’idée à des approximations plus précises.