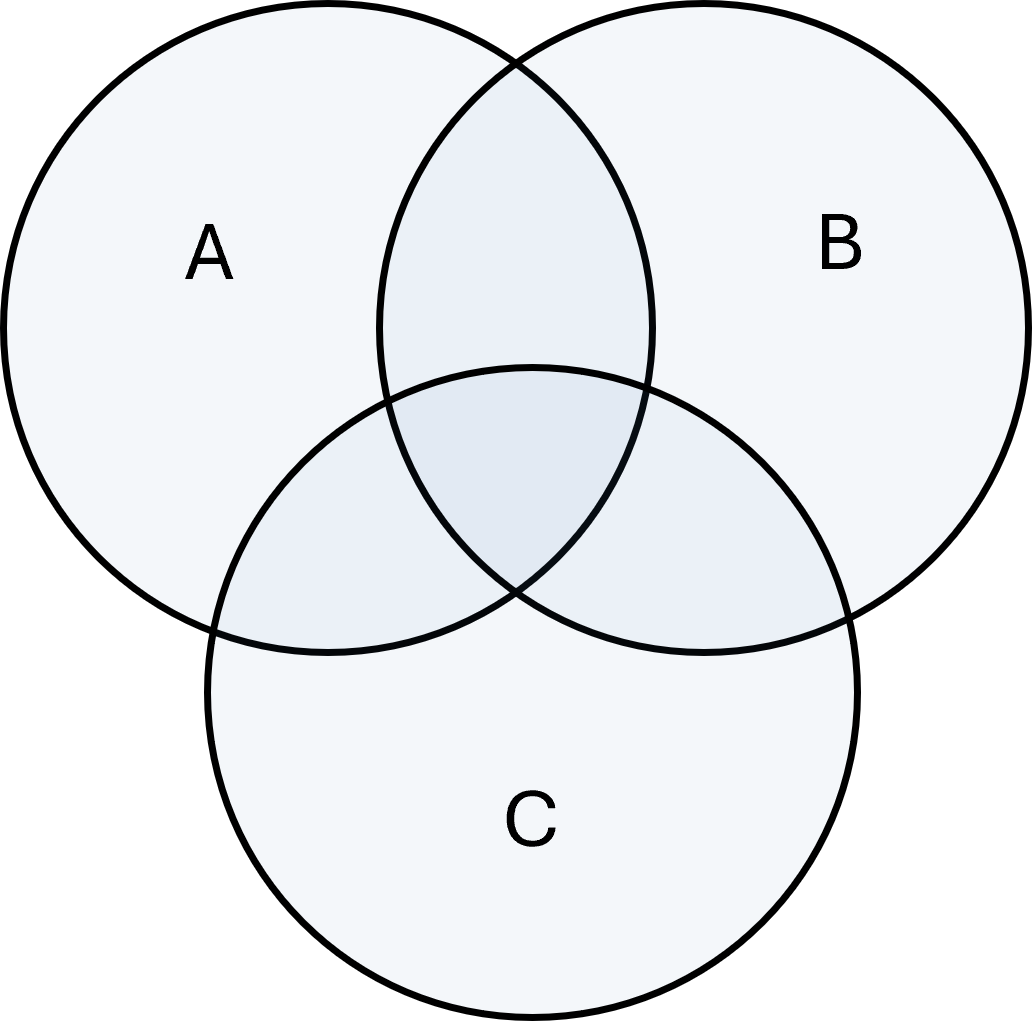
Operaciones con conjuntos
Las operaciones con conjuntos son métodos para combinar o comparar conjuntos. Aquí vemos la unión, la intersección, los conjuntos disjuntos, la diferencia, el complemento y cómo se pueden visualizar con diagramas de Venn.
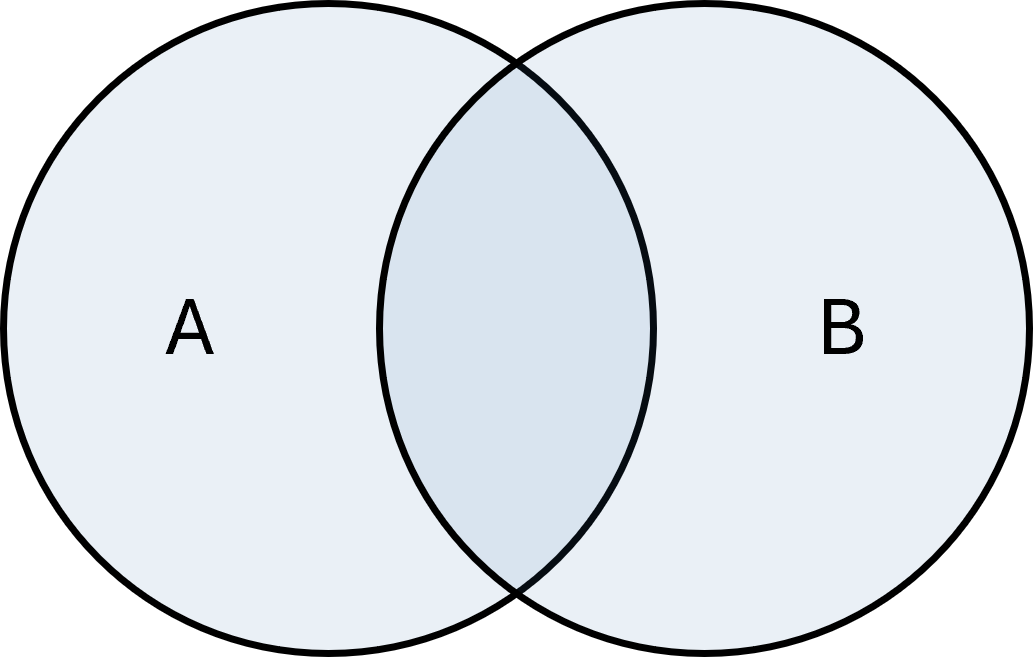
Unión
La unión de dos conjuntos \( \large A\) y \( \large B\) es el conjunto de todos los elementos que están en \( \large A\), en \( \large B\) o en ambos. Se escribe como:
$$ \large A \cup B = \{x \mid x \in A \;\vee\; x \in B\} $$
Ejemplo: Si \( \large A = \{1,2,3\}\) y \( \large B = \{3,4,5\}\), entonces \( \large A \cup B = \{1,2,3,4,5\}\).
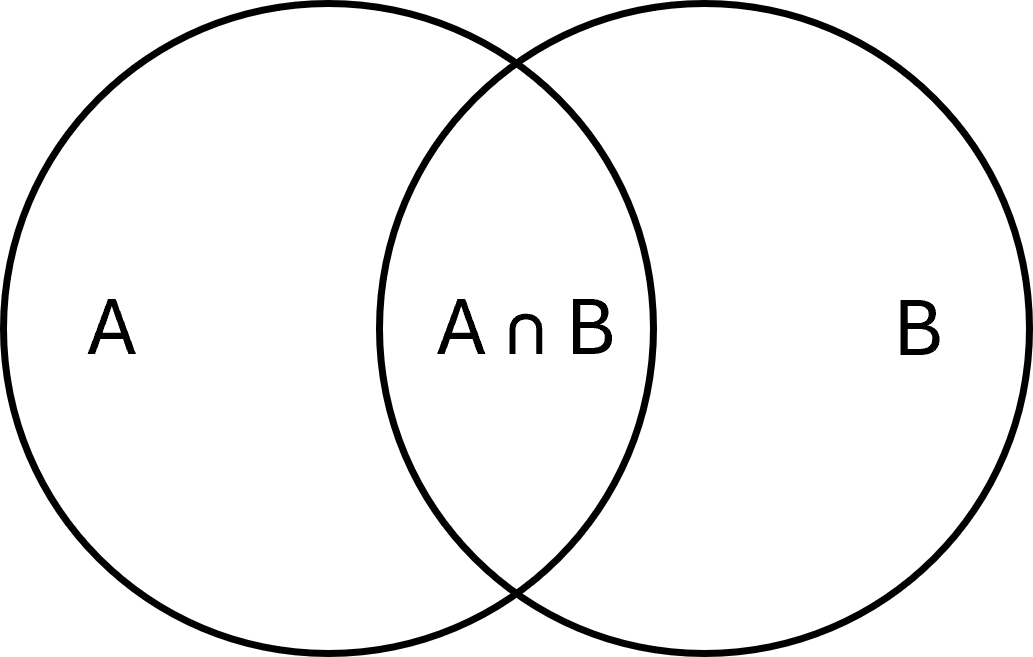
Intersección
La intersección de dos conjuntos son los elementos que tienen en común. Se escribe como:
$$ \large A \cap B = \{x \mid x \in A \;\wedge\; x \in B\} $$
Ejemplo: Si \( \large A = \{1,2,3\}\) y \( \large B = \{3,4,5\}\), entonces \( \large A \cap B = \{3\}\).
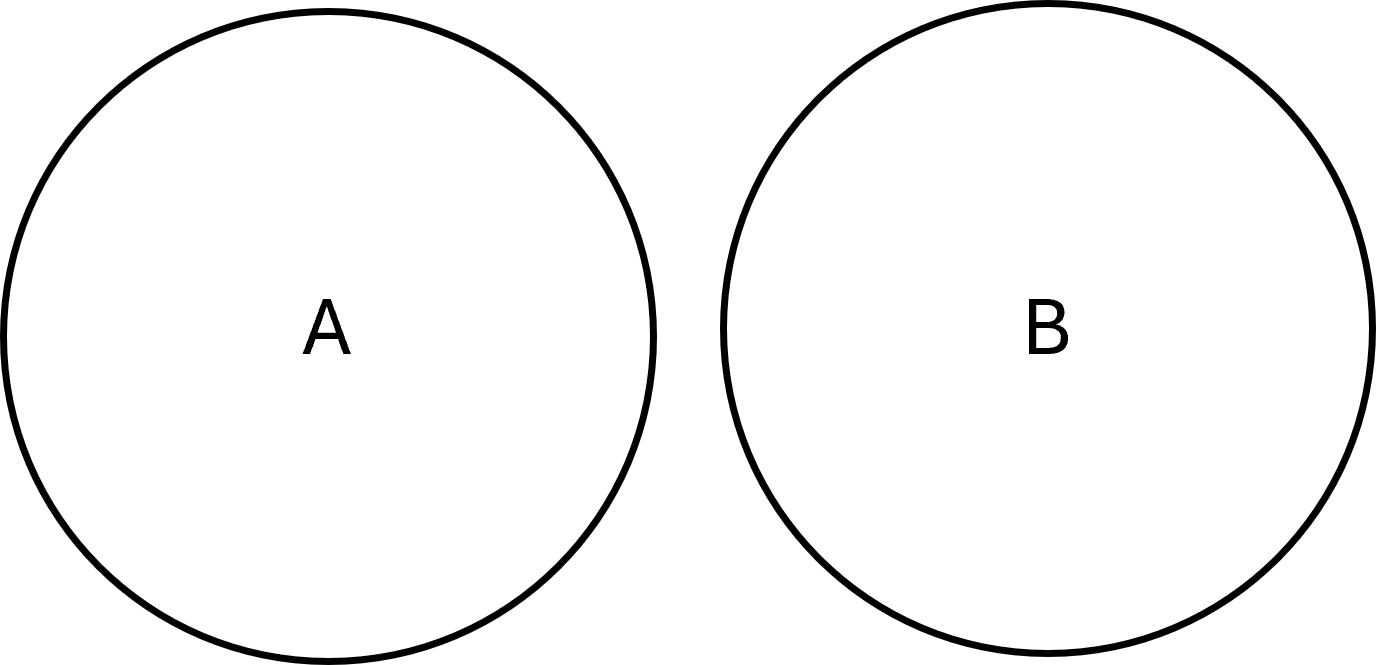
Conjuntos disjuntos
Dos conjuntos son disjuntos si no tienen ningún elemento en común. Es decir, su intersección es vacía:
$$ \large A \cap B = \emptyset $$
Ejemplo: \( \large A = \{1,2,3\}, B = \{4,5,6\}\).
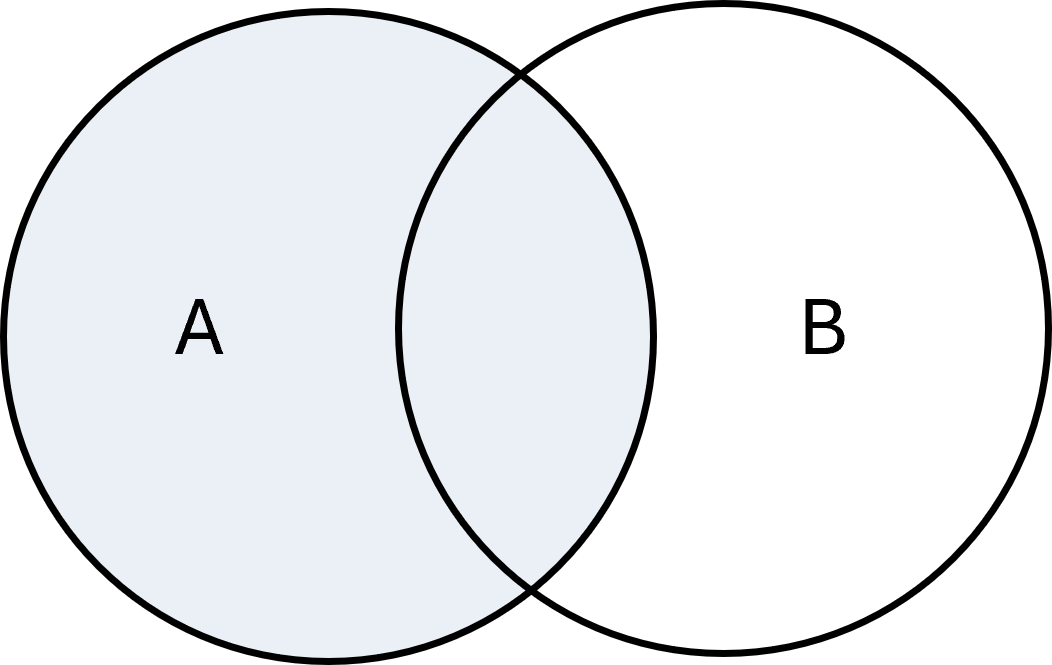
Diferencia
La diferencia de dos conjuntos \( \large A\) y \( \large B\), escrita como \( \large A - B\) o \( \large A \setminus B\), son los elementos que están en \( \large A\) pero no en \( \large B\):
$$ \large A - B = \{x \mid x \in A \;\wedge\; x \notin B\} $$
Ejemplo: Si \( \large A = \{1,2,3\}, B = \{3,4,5\}\), entonces \( \large A - B = \{1,2\}\).
Conjunto complementario
Si tenemos un universo \( \large U\) que contiene todos los elementos posibles, podemos definir el complemento de un conjunto \( \large A\) como todos los elementos de \( \large U\) que no están en \( \large A\). Se escribe como:
$$ \large A^{c} = \{x \in U \mid x \notin A\} $$
Ejemplo: Si \( \large U = \{1,2,3,4,5\}\) y \( \large A = \{1,2\}\), entonces \( \large A^{c} = \{3,4,5\}\).
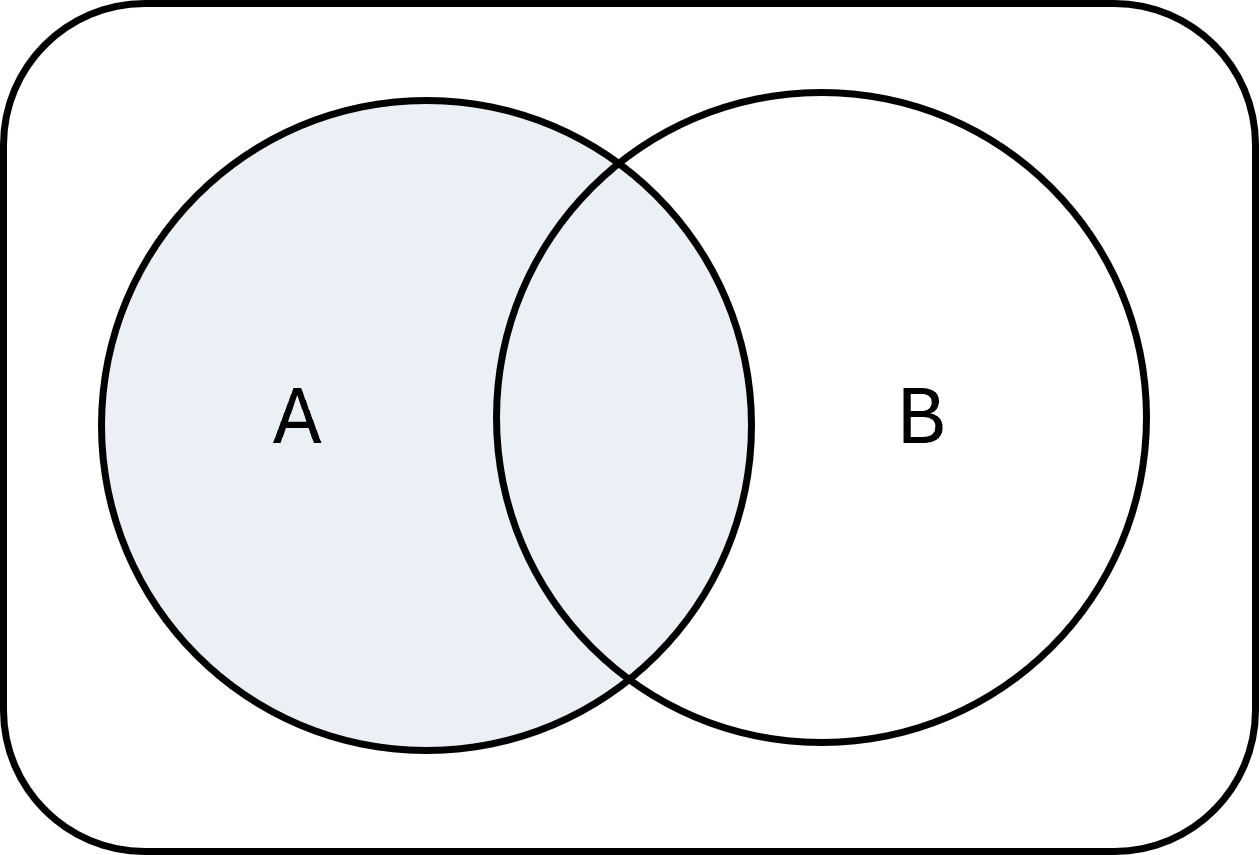
Diagramas de Venn
Los diagramas de Venn se usan a menudo para ilustrar operaciones con conjuntos de manera gráfica.
Los círculos representan conjuntos y las áreas superpuestas muestran cómo funcionan la unión, la intersección, la diferencia y el complemento.