Una parte importante de la teoría de conjuntos es comparar y combinar conjuntos. Aquí vemos subconjuntos, subconjuntos propios, intersecciones, conjuntos potencia y el producto cartesiano.

 

Subconjunto

Un conjunto \( \large A\) es un subconjunto de otro conjunto \( \large B\) si todos los elementos de \( \large A\) también están en \( \large B\). Se escribe así:

 

$$ \large A \subseteq B $$

 

 

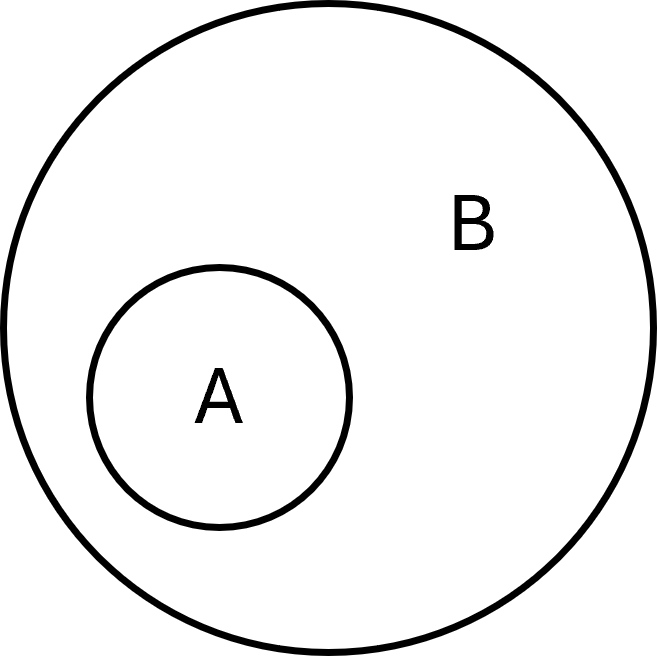
Formalmente se puede definir así:

 

$$ \large A \subseteq B \;\;\Leftrightarrow\;\; \forall x \in A \Rightarrow x \in B $$

 

Ejemplos:

 

• \( \large \{1,2\} \subseteq \{1,2,3,4\}\)
• El conjunto vacío siempre es un subconjunto: \( \large \emptyset \subseteq A\) para cualquier conjunto \( \large A\).

 

Nota: En algunos libros se usa el símbolo \( \large \subset\) en lugar de \( \large \subseteq\) para denotar subconjuntos. Aquí usamos \( \large \subseteq\) como estándar.

 

 

Subconjunto propio

Un conjunto \( \large A\) es un subconjunto propio de \( \large B\) si \( \large A \subseteq B\) pero \( \large A \neq B\).

Esto significa que \( \large B\) contiene al menos un elemento que no está en \( \large A\).

La notación es:

 

$$ \large A \subset B $$

 

Ejemplo: \( \large \{1,2\} \subset \{1,2,3\}\).

 

 

Intersección

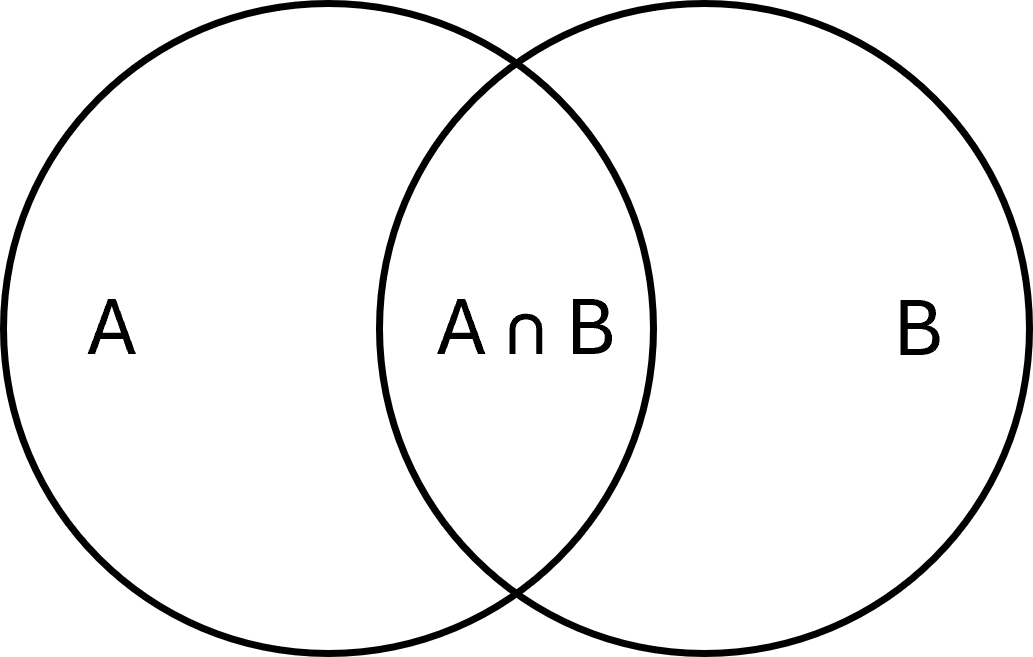
La intersección de dos conjuntos \( \large A\) y \( \large B\) es el conjunto de elementos que están en ambos conjuntos. Se escribe así:

 

$$ \large A \cap B = \{x \mid x \in A \;\wedge\; x \in B\} $$

 

Ejemplo: Si \( \large A = \{1,2,3\}\) y \( \large B = \{3,4,5\}\), entonces \( \large A \cap B = \{3\}\).

 

 

 

 

Conjunto potencia

El conjunto potencia de un conjunto \( \large A\) es el conjunto de todos los subconjuntos de \( \large A\).

El conjunto potencia se escribe \( \large \mathcal{P}(A)\).

 

Si \( \large A = \{0,1\}\), entonces:

 

$$ \large \mathcal{P}(A) = \{\emptyset, \{0\}, \{1\}, \{0,1\}\} $$

 

El número de elementos en un conjunto potencia es \( \large 2^{|A|}\).

Por ejemplo, si \( \large |A| = 3\), entonces \( \large \mathcal{P}(A)\) tiene \( \large 2^3 = 8\) elementos.

 

 

Producto cartesiano

El producto cartesiano de dos conjuntos \( \large A\) y \( \large B\) es el conjunto de todos los pares ordenados donde el primer componente proviene de \( \large A\) y el segundo de \( \large B\).

Se escribe así:

 

$$ \large A \times B = \{(a,b) \mid a \in A \;\wedge\; b \in B\} $$

 

Ejemplo: Si \( \large A = \{1,2\}\) y \( \large B = \{a,b\}\), entonces:

 

$$ \large A \times B = \{(1,a),(1,b),(2,a),(2,b)\} $$

 

Nota que el orden importa: \( \large A \times B \neq B \times A\) en general.