Rectas y planos en el espacio

En el espacio, las rectas y los planos pueden describirse mediante vectores. Esto permite trabajar de forma sistemática con la geometría en tres dimensiones.

 

Rectas

Una recta en el espacio puede describirse mediante un punto \( \large \mathbf{a} \) y un vector de dirección \( \large \mathbf{r} \). Todos los puntos \( \large \mathbf{x} \) de la recta se pueden escribir como

 

$$ \large \mathbf{x} = \mathbf{a} + t \cdot \mathbf{r}, \quad t \in \mathbb{R} $$

 

Aquí, \( \large t \) es un parámetro que determina cuánto se avanza a lo largo de la recta.

 

Ejemplo

Una recta que pasa por el punto \( \large (1,2,0) \) con vector de dirección \( \large (2,-1,3) \) está dada por:

 

$$ \large \mathbf{x} = (1,2,0) + t \cdot (2,-1,3) $$

 

Planos

Un plano puede describirse mediante un punto \( \large \mathbf{a} \) y un vector normal \( \large \mathbf{n} \). Todos los puntos \( \large \mathbf{x} \) en el plano cumplen

 

$$ \large (\mathbf{x} - \mathbf{a}) \cdot \mathbf{n} = 0 $$

 

Esto significa que la diferencia entre cualquier punto del plano y el punto \( \large \mathbf{a} \) es perpendicular al vector normal.

 

Ejemplo

Un plano que pasa por el punto \( \large (1,0,2) \) con vector normal \( \large (2,-1,1) \) puede describirse como

 

$$ \large 2(x-1) -1(y-0) + 1(z-2) = 0 $$

 

o reescrito:

 

$$ \large 2x - y + z = 4 $$

 

Interpretación geométrica

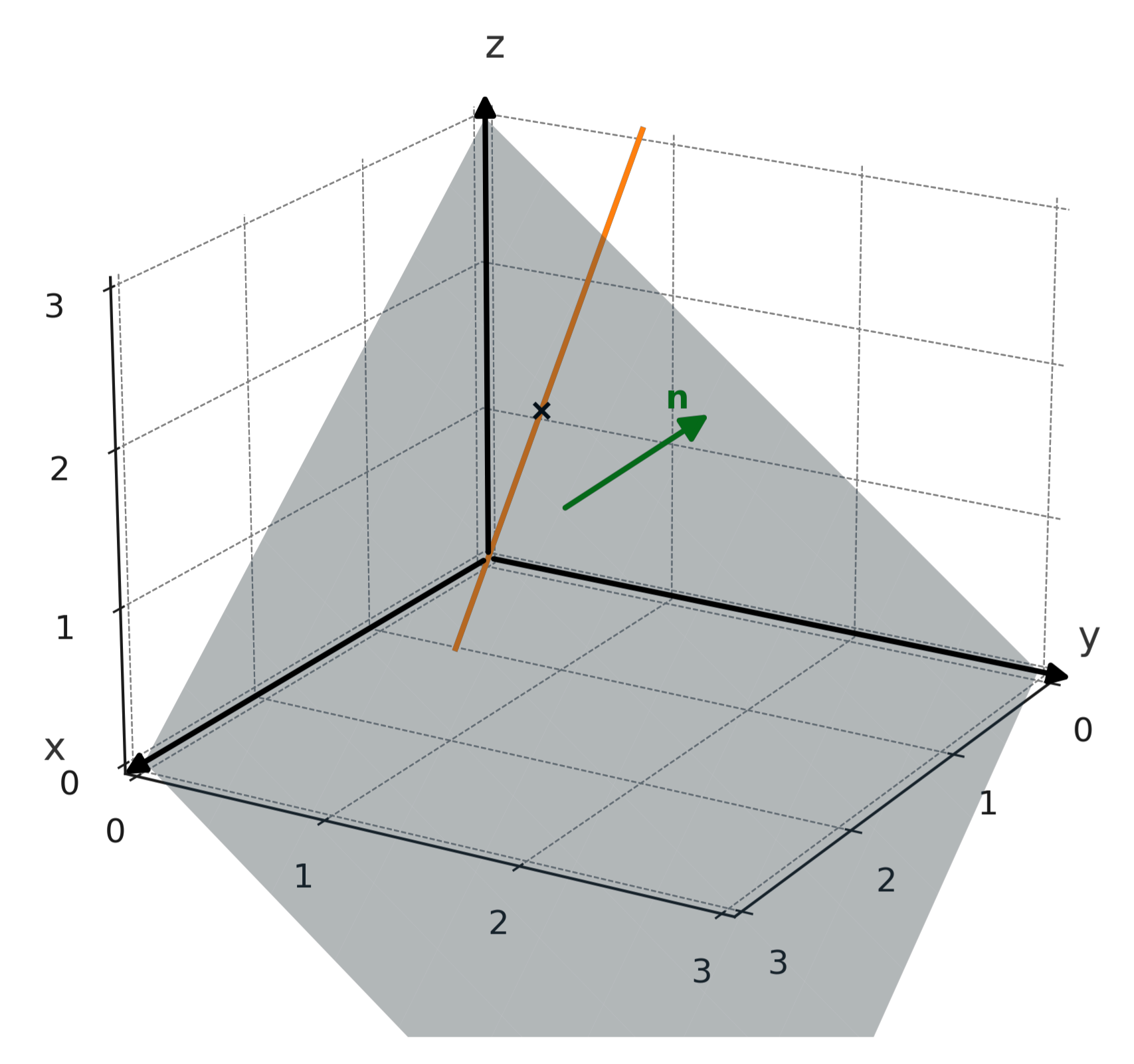
Una recta describe todos los puntos a lo largo de una dirección, mientras que un plano describe todos los puntos en una capa plana infinita. El vector normal (n) a un plano apunta perpendicularmente a esta superficie.

 

La intersección entre una recta y un plano puede ser un único punto, marcado con una cruz en la ilustración de abajo.

También puede ser toda la recta, si la recta yace en el plano, o puede ser vacía, si la recta es paralela y está fuera del plano.

 

 

Aplicación

Las rectas y los planos en el espacio son fundamentales en geometría, física e informática. Se utilizan, por ejemplo, para describir trayectorias, reflexiones, modelado 3D y detección de colisiones en gráficos por computadora.