Volumen con vectores
El volumen de un sólido en el espacio puede calcularse mediante vectores. En particular, los paralelepípedos (cajas) pueden expresarse en una fórmula sencilla cuando se describen con tres vectores.
Volumen de un paralelepípedo
Para tres vectores \( \large \mathbf{u}, \mathbf{v}, \mathbf{w} \) en el espacio, el volumen del paralelepípedo que generan viene dado por:
$$ \large V = \left| \det \begin{pmatrix} x_1 & x_2 & x_3 \\ y_1 & y_2 & y_3 \\ z_1 & z_2 & z_3 \end{pmatrix} \right| $$
donde \( \large \mathbf{u} = (x_1,y_1,z_1) \), \( \large \mathbf{v} = (x_2,y_2,z_2) \) y \( \large \mathbf{w} = (x_3,y_3,z_3) \).
Ejemplo
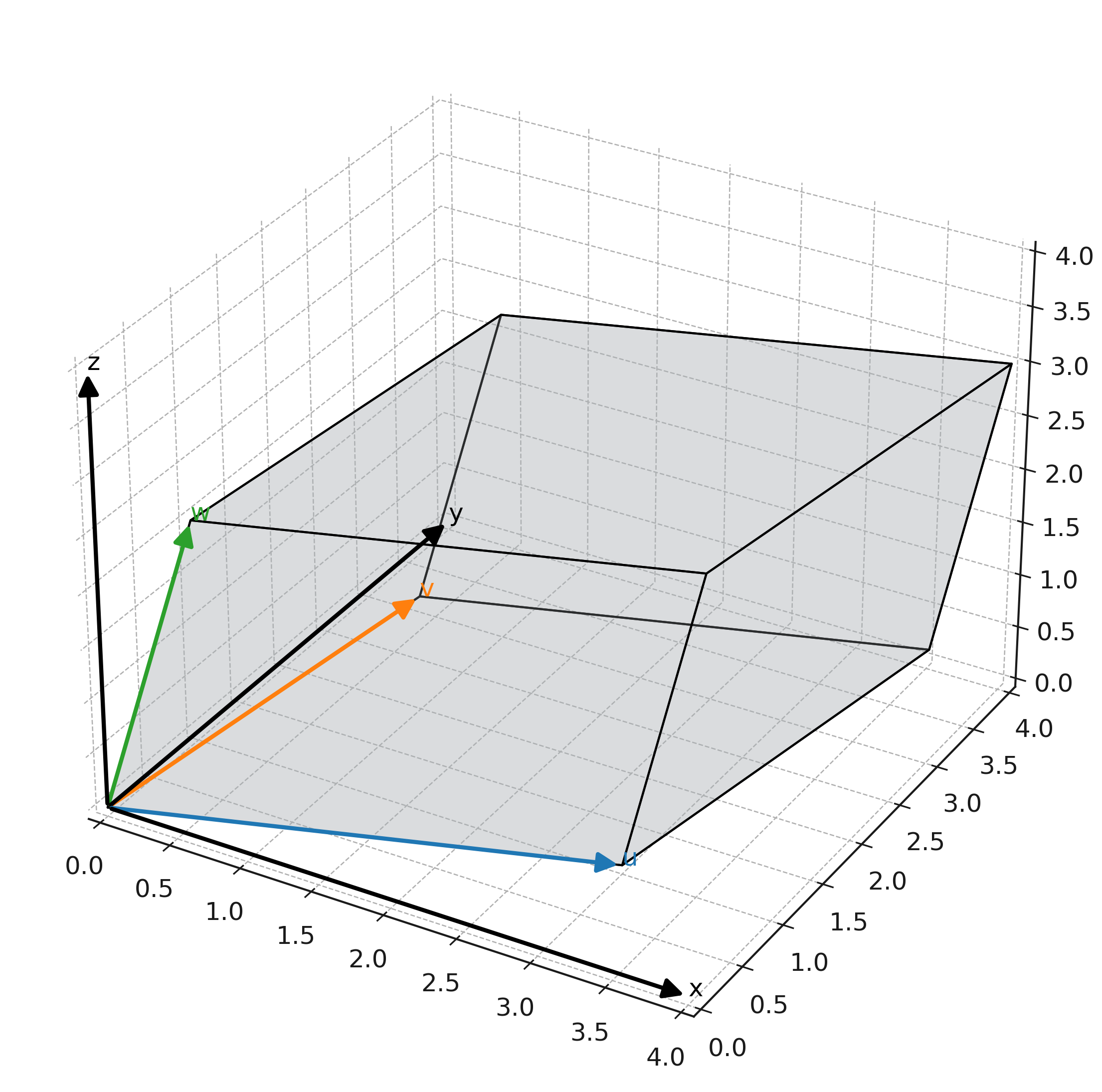
Tomamos \( \large \mathbf{u} = (3,1,0) \), \( \large \mathbf{v} = (1,2,1) \) y \( \large \mathbf{w} = (0,1,2) \).
$$ \large V = \left| \det \begin{pmatrix} 3 & 1 & 0 \\ 1 & 2 & 1 \\ 0 & 1 & 2 \end{pmatrix} \right| $$
Al calcular un determinante, se puede desarrollar por cualquier fila o columna. El resultado siempre es el mismo, independientemente de la que se elija. Para mayor sencillez, aquí desarrollamos por la primera fila.
$$ \large V= 3 \cdot \det \begin{pmatrix} 2 & 1 \\ 1 & 2 \end{pmatrix} - 1 \cdot \det \begin{pmatrix} 1 & 1 \\ 0 & 2 \end{pmatrix} + 0 \cdot \det \begin{pmatrix} 1 & 2 \\ 0 & 1 \end{pmatrix} $$
Los determinantes menores se calculan por separado:
$$ \large \det \begin{pmatrix} 2 & 1 \\ 1 & 2 \end{pmatrix} = 2 \cdot 2 - 1 \cdot 1 = 3 $$
$$ \large \det \begin{pmatrix} 1 & 1 \\ 0 & 2 \end{pmatrix} = 1 \cdot 2 - 1 \cdot 0 = 2 $$
Sustituimos ahora los resultados en la expresión:
$$ \large V = | 3 \cdot 3 - 1 \cdot 2 + 0 | = | 9 - 2 | = | 7 | = 7 $$
El volumen del paralelepípedo es por tanto 7. Usamos el valor absoluto porque un determinante puede ser negativo según la orientación de los vectores, pero el volumen nunca puede ser menor que cero.
Interpretación geométrica
La fórmula corresponde a calcular área de la base por altura. El área de la base se obtiene mediante un cálculo de área, y la altura se obtiene proyectando el tercer vector perpendicularmente sobre la base.
Aplicación
Las fórmulas de volumen con vectores se utilizan en geometría, álgebra lineal y física. Permiten calcular el volumen de cajas y otros sólidos en sistemas de coordenadas, y forman la base de temas posteriores como determinantes, el producto vectorial e integrales.