Producto vectorial
El producto vectorial de dos vectores en el espacio es un vector que es perpendicular a ambos vectores originales. El producto vectorial se utiliza para encontrar áreas, vectores normales y orientaciones en la geometría 3D.
Definición
Para dos vectores \( \large \mathbf{u} = (x_1,y_1,z_1) \) y \( \large \mathbf{v} = (x_2,y_2,z_2) \), el producto vectorial se define mediante el determinante:
$$ \large \mathbf{u} \times \mathbf{v} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end{vmatrix} = (y_1z_2 - z_1y_2,\; z_1x_2 - x_1z_2,\; x_1y_2 - y_1x_2) $$
Ejemplo
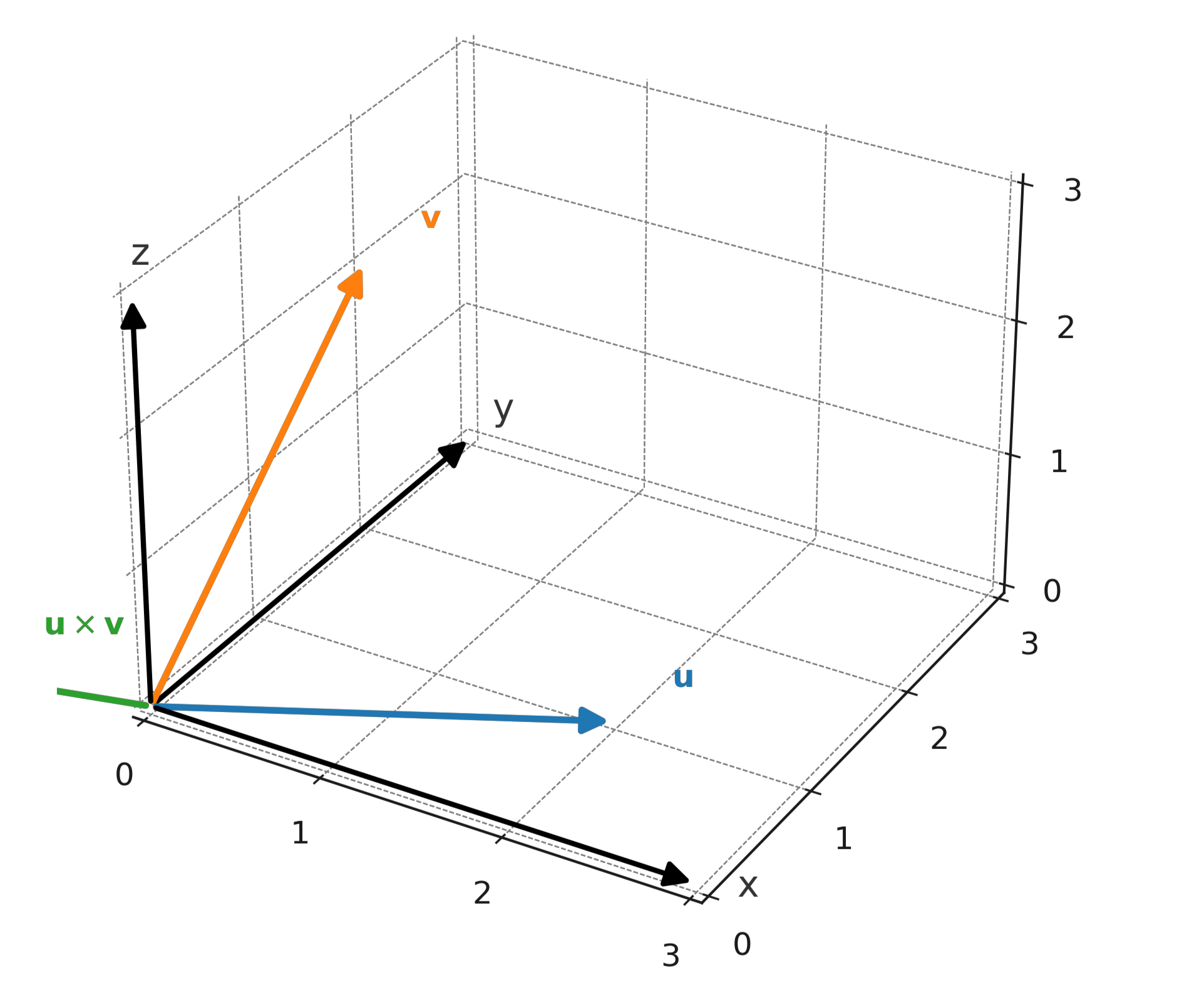
Tomamos \( \large \mathbf{u} = (1,2,3) \) y \( \large \mathbf{v} = (4,5,6) \).
$$ \large \mathbf{u} \times \mathbf{v} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 1 & 2 & 3 \\ 4 & 5 & 6 \end{vmatrix} = (-3,6,-3) $$
El resultado es un nuevo vector \( \large (-3,6,-3) \), que es perpendicular tanto a \( \large \mathbf{u} \) como a \( \large \mathbf{v} \).
Interpretación geométrica
La longitud del producto vectorial corresponde al área del paralelogramo definido por los vectores:
$$ \large |\mathbf{u} \times \mathbf{v}| = |\mathbf{u}| \cdot |\mathbf{v}| \cdot \sin(\theta) $$
La dirección se determina mediante la regla de la mano derecha: Si se apunta con el dedo índice de la mano derecha en la dirección de \( \large \mathbf{u} \) y con el dedo medio en la dirección de \( \large \mathbf{v} \), entonces el pulgar apunta en la dirección de \( \large \mathbf{u} \times \mathbf{v} \).
Aplicación
El producto vectorial se utiliza en muchos campos de las matemáticas y la física:
- Para encontrar un vector normal a un plano
- Para calcular el área de paralelogramos y triángulos en 3D
- En mecánica para determinar el momento de una fuerza
- En gráficos por computadora para calcular la orientación de superficies