Producto escalar

El producto escalar es una operación entre dos vectores que da un número. Se utiliza para calcular ángulos entre vectores y para determinar si son perpendiculares.

 

Definición

Para dos vectores en el espacio \( \large \mathbf{u} = (x_1,y_1,z_1) \) y \( \large \mathbf{v} = (x_2,y_2,z_2) \), el producto escalar se define como

 

$$ \large \mathbf{u} \cdot \mathbf{v} = x_1x_2 + y_1y_2 + z_1z_2 $$

 

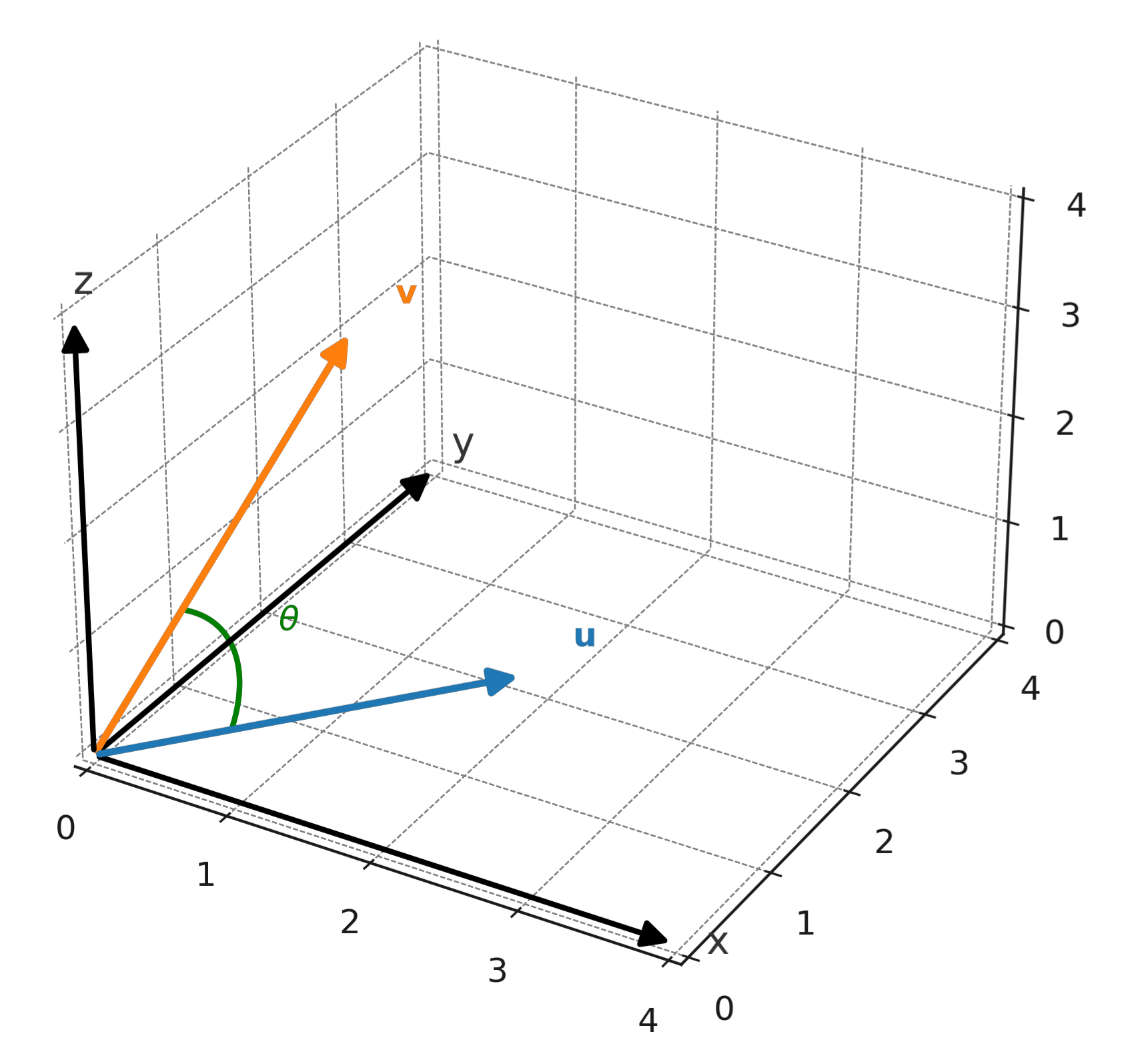
Otra fórmula muestra la relación con el ángulo entre los vectores:

 

$$ \large \mathbf{u} \cdot \mathbf{v} = |\mathbf{u}| \cdot |\mathbf{v}| \cdot \cos(\theta) $$

 

donde \( \large \theta \) es el ángulo entre \( \large \mathbf{u} \) y \( \large \mathbf{v} \).

 

 

Ejemplo

Tomamos \( \large \mathbf{u} = (1,2,3) \) y \( \large \mathbf{v} = (4,-1,2) \).

 

$$ \large \mathbf{u} \cdot \mathbf{v} = 1 \cdot 4 + 2 \cdot (-1) + 3 \cdot 2 = 4 - 2 + 6 = 8 $$

 

El producto escalar es 8.

 

 

Interpretación geométrica

El producto escalar mide cuánto apuntan los dos vectores en la misma dirección. Si el ángulo es menor que 90°, el producto escalar es positivo. Si el ángulo es mayor que 90°, el producto escalar es negativo. Si los vectores son perpendiculares, el producto escalar es cero.

 

 

Aplicación

El producto escalar se utiliza en muchos contextos, entre ellos para encontrar ángulos entre vectores, determinar ortogonalidad y en física para calcular el trabajo realizado por una fuerza a lo largo de un desplazamiento.