Coordenadas en 3D
En el espacio 3D, un punto se describe mediante tres coordenadas. Mientras que en el plano usamos dos números para indicar una posición, en el espacio se requieren tres números para determinar un punto de manera única.
Definición
Un punto \( \large P \) en el espacio se expresa como
$$ \large P = (x,y,z) $$
Aquí \( \large x \) es la distancia a lo largo del eje x, \( \large y \) la distancia a lo largo del eje y, y \( \large z \) la distancia a lo largo del eje z.
Ejemplo
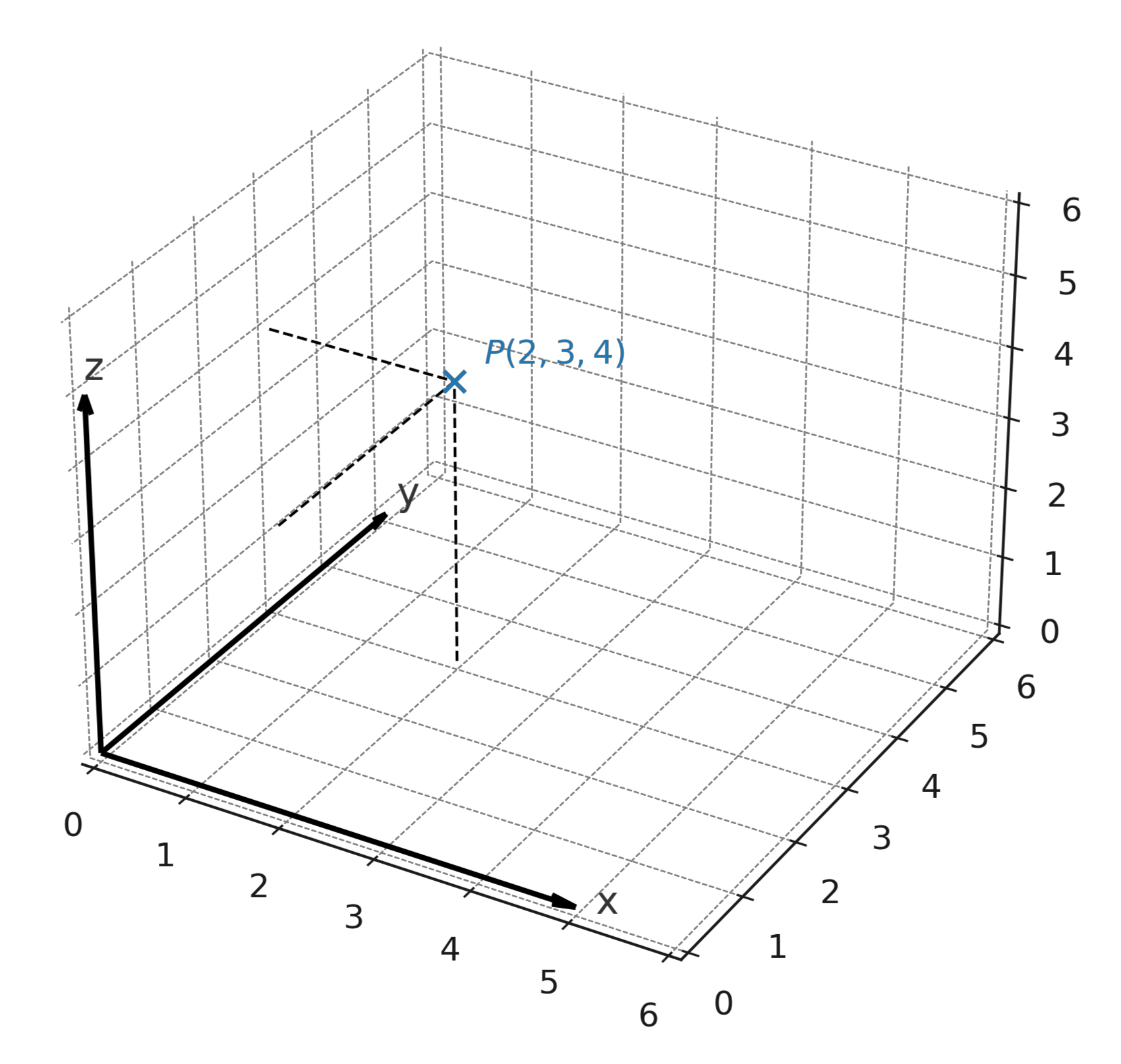
El punto \( \large P = (2,3,4) \) significa avanzar 2 unidades a lo largo del eje x, 3 unidades a lo largo del eje y y 4 unidades hacia arriba a lo largo del eje z.
Ejes coordenados y origen
Los tres ejes se llaman eje x, eje y y eje z. Su punto de inicio común se llama origen y tiene las coordenadas
$$ \large O = (0,0,0) $$
Un vector desde el origen hasta un punto \( \large P=(x,y,z) \) se escribe como
$$ \large \vec{OP} = (x,y,z) $$
Distancia en el espacio
La distancia desde el origen hasta un punto \( \large (x,y,z) \) se obtiene extendiendo el teorema de Pitágoras:
$$ \large |(x,y,z)| = \sqrt{x^2 + y^2 + z^2} $$
Esto es la longitud del vector desde el origen hasta el punto.
Interpretación geométrica
Un sistema de coordenadas en el espacio se construye con tres ejes mutuamente perpendiculares. Cada punto puede verse como una esquina de un prisma rectangular con el origen como punto de partida.
Aplicación
Las coordenadas en 3D se utilizan en todas partes en matemáticas, física e informática, por ejemplo para describir puntos en geometría, posiciones en el espacio u objetos en gráficos 3D.