Probabilidad estadística

La probabilidad se puede calcular de dos maneras: teórica (clásica) y estadística (empírica).

 

Probabilidad clásica

Si se conoce el espacio muestral y todos los resultados son igualmente probables, se puede usar la fórmula:

 

$$ \large P(A) = \frac{\text{número de resultados favorables}}{\text{número de resultados posibles}} $$

 

Ejemplo: La probabilidad de sacar un seis con un dado es:

 

$$ \large \frac{1}{6} \approx 0.167 = 16.7\% $$

 

 

Probabilidad estadística (empírica)

A veces no se puede calcular la probabilidad directamente. En su lugar, se realizan ensayos o experimentos y se usan las observaciones para calcular la probabilidad.

 

Ejemplo: Lanzamos un dado 1.000 veces y registramos frecuencia absoluta y relativa:

 

	1	2	3	4	5	6
$$ h(x) $$	$$ 180 $$	$$ 176 $$	$$ 149 $$	$$ 170 $$	$$ 167 $$	$$ 158 $$
$$ f(x) $$	$$ \tfrac{180}{1000} $$	$$ \tfrac{176}{1000} $$	$$ \tfrac{149}{1000} $$	$$ \tfrac{170}{1000} $$	$$ \tfrac{167}{1000} $$	$$ \tfrac{158}{1000} $$
Esperado	$$ \tfrac{1000}{6} \approx 167 $$	$$ 167 $$	$$ 167 $$	$$ 167 $$	$$ 167 $$	$$ 167 $$

 

 

Diagrama

El diagrama de barras siguiente muestra la probabilidad teórica (167 para cada cara) comparada con los resultados empíricos.

 

 

 

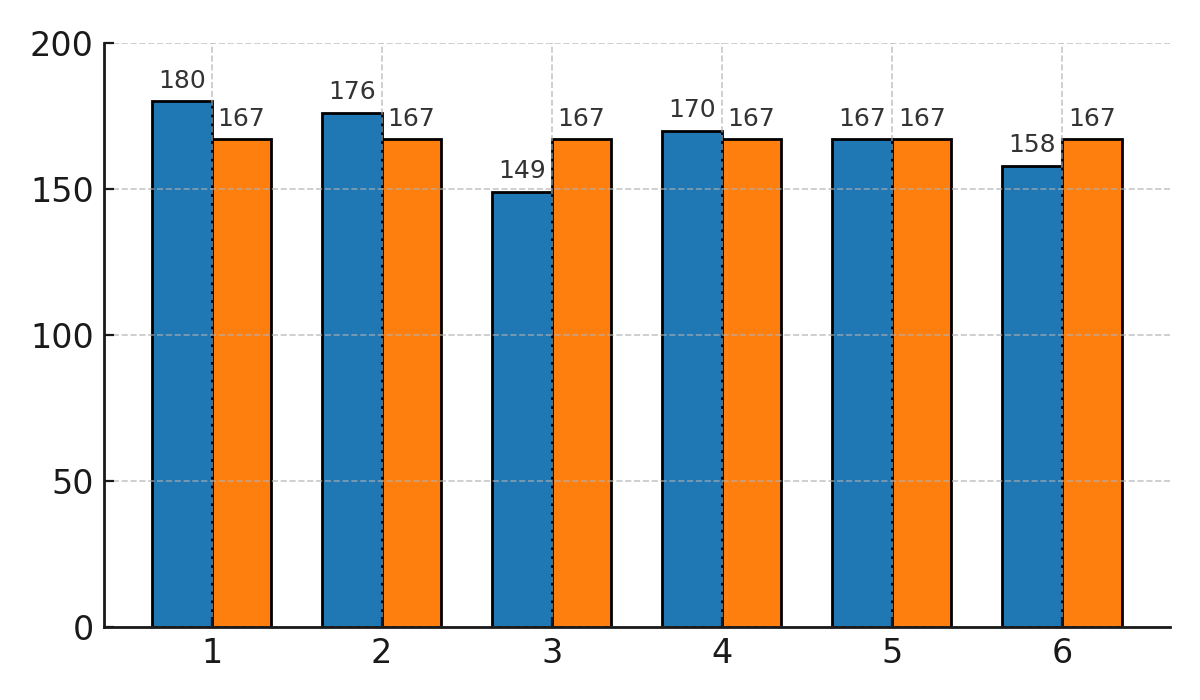
Comparación

Sabemos que la probabilidad de sacar un seis es:

 

$$ \large \tfrac{1}{6} \approx 0.167 = 16.7\% $$

 

En cambio, nuestro experimento mostró:

 

$$ \large \tfrac{158}{1000} = 0.158 = 15.8\% $$

 

El resultado no es exactamente el mismo que el valor teórico, pero está cerca. Esto muestra cómo se usa la probabilidad estadística para aproximarse a la probabilidad teórica a través de observaciones.

 

La probabilidad estadística es por tanto una herramienta práctica cuando no se puede calcular la probabilidad directamente, sino que hay que basarse en observaciones.