Ley de los grandes números

La ley de los grandes números es un principio fundamental en la teoría de la probabilidad.

Afirma que cuanto más veces se repite un experimento, más cercanos estarán los resultados observados a la probabilidad teórica.

 

 

Ejemplo con un dado

Si lanzas un dado una vez, no hay garantía de obtener un seis.

Si lo lanzas 6 veces, puede ocurrir perfectamente que no salga ningún seis.

Si lo lanzas 1.000 veces, normalmente se observa que alrededor de un sexto de los lanzamientos da como resultado un seis – es decir, unas 167 veces.

 

 

Probabilidad teórica

Sabemos que la probabilidad de obtener un seis es:

 

$$ P(\text{seis}) = \tfrac{1}{6} \approx 0,167 = 16,7\% $$

 

Probabilidad estadística

En un experimento con 1.000 lanzamientos podemos obtener el resultado:

 

• Número de seises: 158
• Probabilidad estadística: \( \tfrac{158}{1000} = 0,158 = 15,8\% \)

 

Esto está cerca del valor teórico del 16,7%.

 

 

 

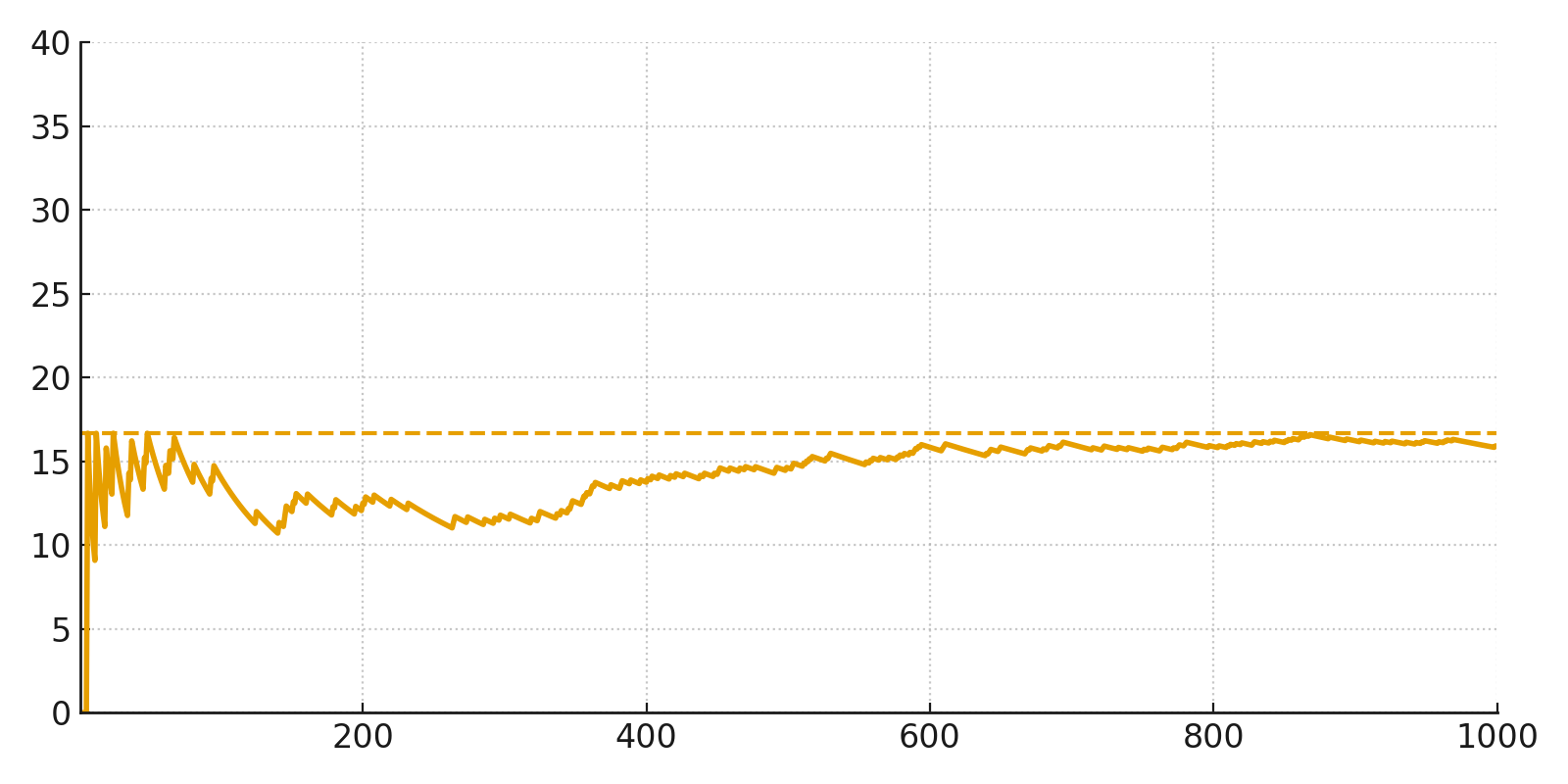
Aquí lanzamos un dado 1.000 veces y seguimos el porcentaje de lanzamientos que dieron un seis.

Al principio la curva fluctúa mucho, pero a medida que aumenta el número de lanzamientos, se estabiliza alrededor de la probabilidad teórica de aproximadamente 16,7%.

Esto es exactamente lo que significa la ley de los grandes números: las probabilidades solo tienen sentido cuando tenemos muchas observaciones.

 

 

Importancia

La ley de los grandes números muestra por qué las probabilidades tienen sentido en la práctica:

 

• Los conjuntos de datos pequeños pueden dar fluctuaciones aleatorias.
• Los conjuntos de datos grandes ofrecen una imagen más fiable.

 

 

Resumen

• La ley de los grandes números se aplica a muchas repeticiones de un experimento.
• Las frecuencias empíricas se aproximan a las probabilidades teóricas.
• Cuanto mayor sea la muestra, más preciso será el resultado.