Varianza y desviación estándar
Dispersión
La dispersión indica cuánto varían las observaciones alrededor de la media.
Si todas las observaciones están cerca de la media, la dispersión es pequeña. Si están lejos de la media, la dispersión es grande.
Varianza
La varianza mide la distancia media al cuadrado respecto a la media.
Para encontrar la varianza debes:
- Restar la media a cada observación
- Elevar al cuadrado las diferencias
- Calcular la media de las diferencias al cuadrado
$$ s^2 = \frac{(x_1 - \overline{x})^2 + (x_2 - \overline{x})^2 + ... + (x_n - \overline{x})^2}{n} $$
Desviación estándar
La desviación estándar es la raíz cuadrada de la varianza. Indica, en la misma unidad que las observaciones, cuánto se desvían típicamente de la media.
$$ s = \sqrt{s^2} $$
Ejemplo
Usamos la observación de las estaturas de los alumnos.
- La media es \( \overline{x} = 164{,}8 \)
- La varianza es \( s^2 = 40{,}36 \)
- La desviación estándar es \( s \approx 6{,}35 \)
Esto significa que las estaturas se desvían en promedio unos 6,35 cm de la media.
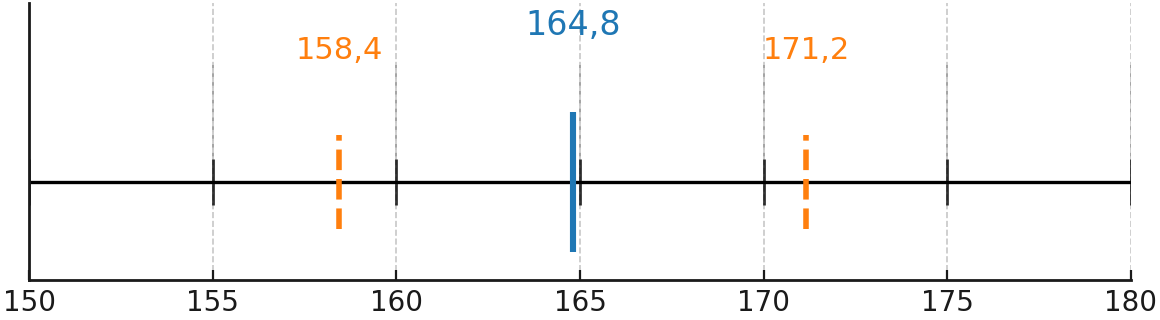
Diagrama
La desviación estándar se puede mostrar en un diagrama, donde se marca la media y se indican los intervalos \( \overline{x} \pm s \).