Integral definida
La integral definida se utiliza para calcular la cantidad total de una función entre dos puntos. Mientras que la integral indefinida describe todas las primitivas, la integral definida da un número que representa el valor acumulado — a menudo un área.
Definición
La integral definida de una función \( \large f(x) \) desde \( \large a \) hasta \( \large b \) se define como el límite de la suma de muchos pequeños rectángulos bajo la gráfica:
$$ \large \int_a^b f(x)\,dx \;=\; \lim_{n \to \infty} \sum_{i=1}^{n} f(x_i)\,\Delta x $$
Cada término de la suma representa el área de un pequeño rectángulo con altura \( \large f(x_i) \) y anchura \( \large \Delta x \). A medida que aumenta el número de rectángulos, la aproximación se vuelve más precisa y, en el límite, se obtiene el área exacta.
Interpretación geométrica
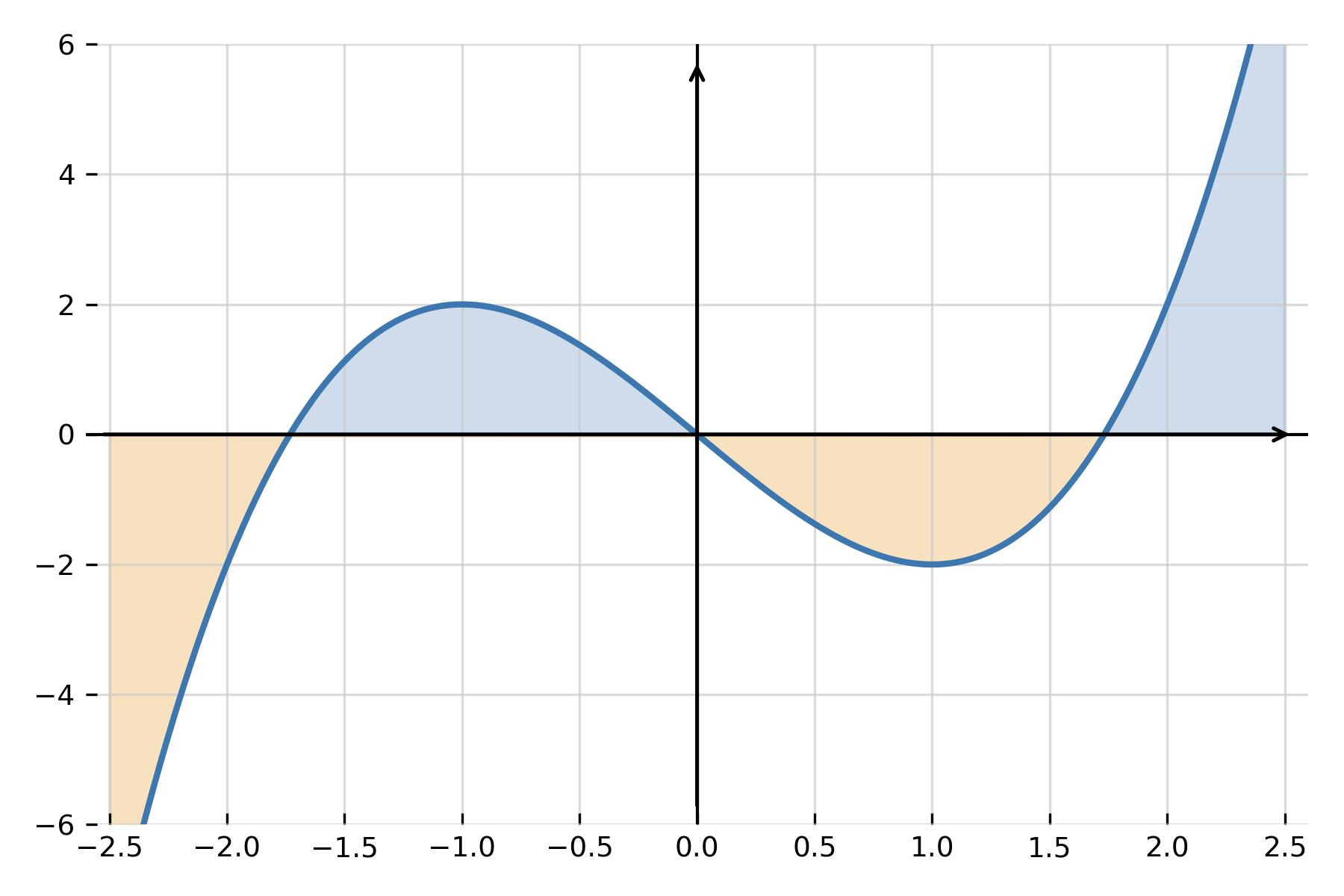
Si \( \large f(x) \ge 0 \) en el intervalo, la integral definida representa el área entre la gráfica y el eje x. Si la función cruza el eje x, las regiones bajo el eje se cuentan como negativas, por lo que la integral muestra el área neta.
Teorema fundamental
Existe una relación estrecha entre las primitivas y las integrales definidas. Si \( \large F \) es una primitiva de \( \large f \), el teorema fundamental del cálculo establece:
$$ \large \int_a^b f(x)\,dx \;=\; F(b) - F(a) $$
Esto significa que se puede encontrar una integral definida sin calcular sumas de Riemann. En su lugar, se encuentra una primitiva y se restan los valores de la función en los dos límites.
Ejemplo 1: Área bajo la gráfica
Calcular el área bajo \( \large f(x) = x^2 \) desde \( \large x=0 \) hasta \( \large x=3 \):
$$ \large \int_0^3 x^2\,dx \;=\; \Big[\tfrac{1}{3}x^3\Big]_0^3 \;=\; \tfrac{1}{3}\cdot 27 - 0 \;=\; 9 $$
El área bajo la gráfica es por tanto de 9 unidades.
Ejemplo 2: Contribución negativa y positiva
Calcular \( \large \int_{-1}^{2} (x-1)\,dx \):
$$ \large \int_{-1}^{2} (x-1)\,dx \;=\; \Big[\tfrac{1}{2}x^2 - x\Big]_{-1}^{2} \;=\; \big(2 - 2\big) - \big(\tfrac{1}{2} - (-1)\big) = -\tfrac{3}{2} $$
La integral es negativa porque la función está por debajo del eje x en parte del intervalo. La integral definida mide por tanto la acumulación neta, no solo la suma de las áreas positivas.
Signo y cantidad acumulada
Una integral positiva significa que la función está en promedio por encima del eje x en el intervalo. Una integral negativa significa lo contrario. En física y economía, esto se interpreta como superávit o déficit en una cantidad total.
Interpretación gráfica
La integral definida puede entenderse como la suma de áreas con signo. Por tanto, puede visualizarse como el área entre la gráfica y el eje x, donde las áreas bajo el eje se restan.
Resumen
La integral definida da un número que representa el cambio total, la cantidad acumulada o el área neta de una función entre dos límites. Puede obtenerse geométricamente como un área o algebraicamente mediante las primitivas y el teorema fundamental.