Aplicaciones del cálculo integral
Las integrales no solo se utilizan para calcular áreas, sino también en muchos contextos diferentes donde es necesario sumar pequeñas contribuciones para obtener una cantidad total. En física, economía y geometría, las integrales proporcionan una herramienta matemática precisa para medir el crecimiento total, la energía, la masa, la distancia o el volumen.
Área entre dos curvas
Una de las aplicaciones más comunes es encontrar el área entre dos funciones \( \large f(x) \) y \( \large g(x) \). Si \( \large f(x) \ge \large g(x) \) en el intervalo \([ \large a,\large b ]\), el área se calcula como la diferencia entre ambas:
$$ \large A \;=\; \int_a^b \big(f(x) - g(x)\big)\,dx $$
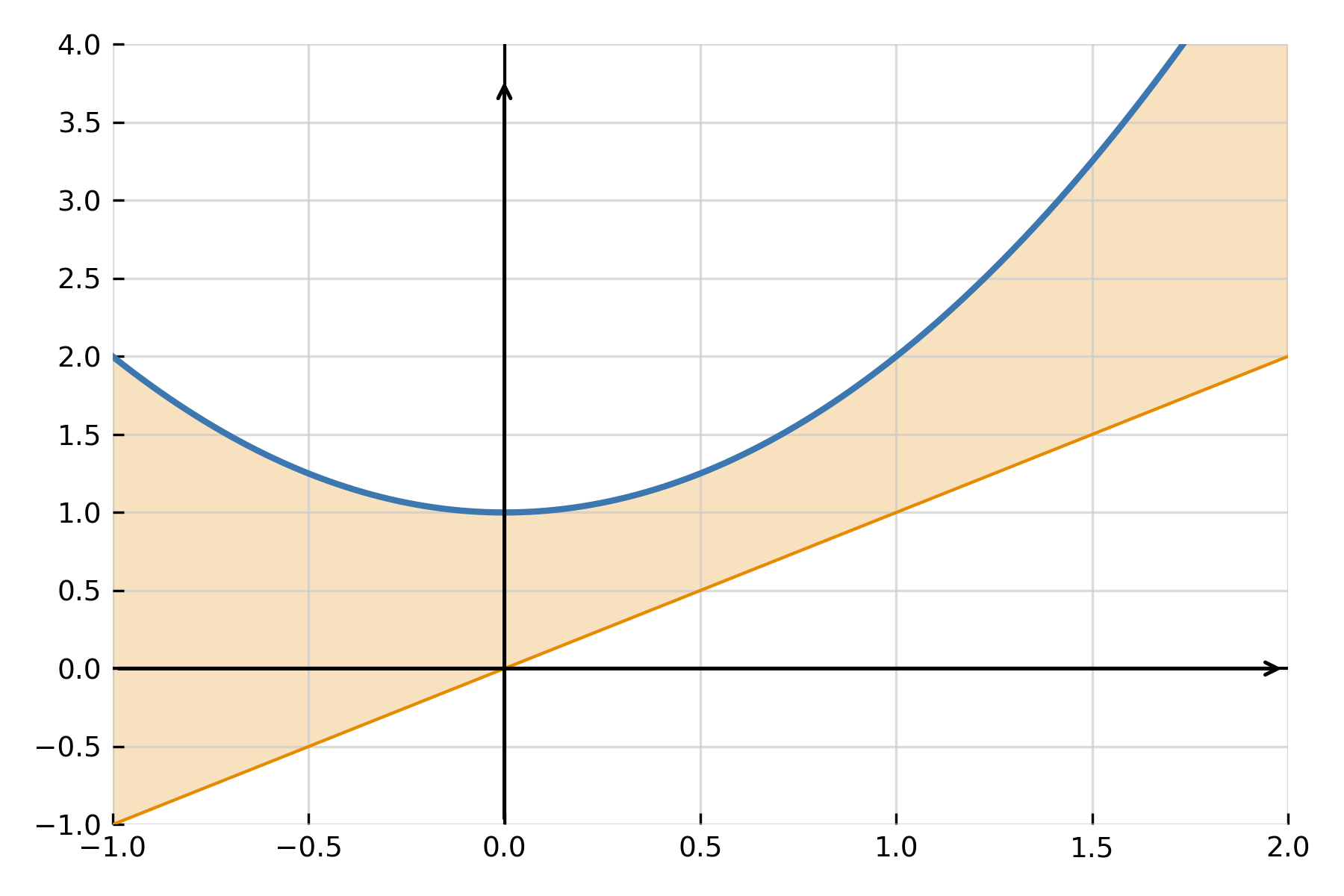
La integral mide exactamente la distancia vertical entre las curvas para cada \( \large x \) y la suma a lo largo del intervalo. Si las gráficas se cruzan, el intervalo se divide en partes tomando siempre la diferencia positiva.
Volumen de sólidos de revolución
Cuando una función gira alrededor del eje x, forma un sólido tridimensional. El volumen puede encontrarse sumando las áreas de las secciones transversales (discos) a lo largo del eje:
$$ \large V \;=\; \pi \int_a^b \big(f(x)\big)^2\,dx $$
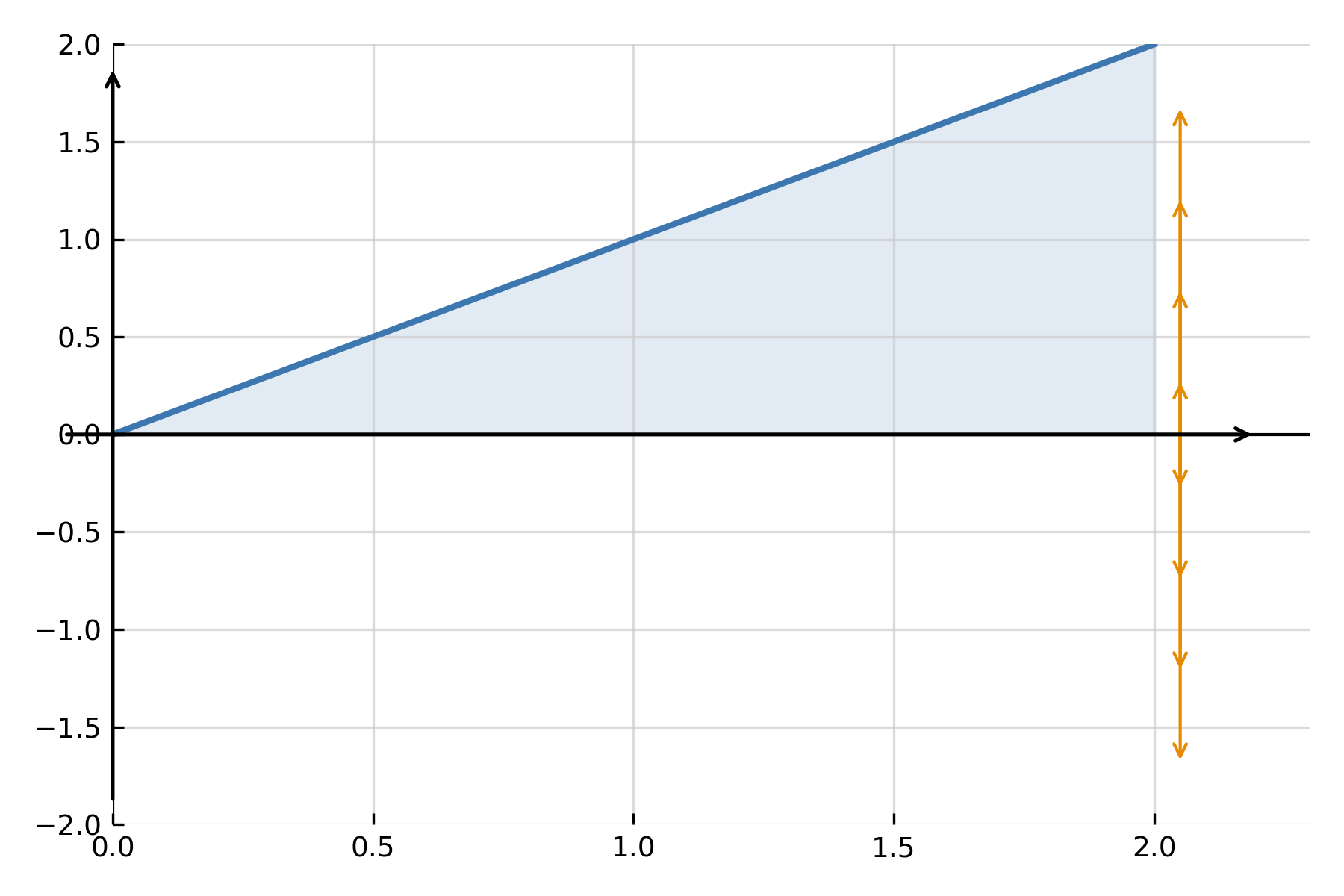
Aquí, \( \large f(x) \) es el radio de la función rotada en el punto \( \large x \). La integral suma infinitos discos pequeños que, en conjunto, forman el volumen total.
Ejemplo: Sólido de revolución
Encuentra el volumen del sólido formado al girar \( \large f(x)=x \) alrededor del eje x desde \( \large x=0 \) hasta \( \large x=2 \):
$$ \large V \;=\; \pi \int_0^2 x^2\,dx \;=\; \pi \Big[\tfrac{1}{3}x^3\Big]_0^2 \;=\; \tfrac{8}{3}\pi $$
Esto corresponde al volumen de un cono con altura 2 y radio 2.
Trabajo y energía
En física, las integrales se usan para calcular el trabajo cuando una fuerza varía con la posición. El trabajo \( \large W \) es la suma de pequeñas contribuciones de fuerza \( \large F(x)\,dx \):
$$ \large W \;=\; \int_a^b F(x)\,dx $$
Si la fuerza es constante, esto se reduce a \( \large W = F \cdot s \), pero la integral permite calcular cuando la fuerza cambia a lo largo del movimiento.
Movimiento y distancia recorrida
Cuando se conoce la función de velocidad \( \large v(t) \) de un objeto, la integral de \( \large v(t) \) da la distancia recorrida:
$$ \large s \;=\; \int_{t_1}^{t_2} v(t)\,dt $$
Si la velocidad puede ser negativa (movimiento hacia atrás), se debe integrar con signo. Si se desea la distancia total sin importar la dirección, se usa \( \large \int |v(t)|\,dt \).
Aplicaciones económicas y biológicas
Las integrales también se utilizan para calcular el crecimiento acumulado, el consumo o los ingresos a lo largo del tiempo. En economía, \( \large f(x) \) puede representar una función marginal, por ejemplo el ingreso por unidad, y la integral da el ingreso total. En biología, las integrales se utilizan para medir la biomasa total, la absorción de energía o la cantidad de sustancia de una población.
Valor promedio de una función
El valor promedio de una función en un intervalo se encuentra tomando el área total y dividiéndola por la longitud del intervalo:
$$ \large f_{\text{avg}} \;=\; \frac{1}{b-a}\int_a^b f(x)\,dx $$
Esta fórmula se utiliza en estadística, física y análisis para encontrar valores medios de funciones continuas.
Cuando una integral no puede calcularse analíticamente, se pueden usar métodos numéricos como el método del rectángulo, el método del trapecio o la regla de Simpson para encontrar un valor aproximado. Estos métodos se describen en la sección Métodos numéricos.
Resumen
Las integrales se utilizan para calcular áreas, volúmenes, energía, trabajo y mucho más. Lo que todas las aplicaciones tienen en común es que la integral suma pequeñas partes en una cantidad total. Así, el cálculo integral constituye una herramienta central para describir y calcular relaciones en la naturaleza, la ingeniería y la economía.