Cálculo integral
El cálculo integral trata de sumar pequeñas contribuciones para obtener una cantidad total. Mientras el cálculo diferencial mide los cambios instantáneos (\( \large \text{pendientes} \)), el cálculo integral mide las cantidades acumuladas como el área, la distancia, el crecimiento total o la energía. Las dos ramas están estrechamente relacionadas: derivar e integrar son procesos inversos.
Qué es el cálculo integral
Cuando una magnitud cambia gradualmente, se puede imaginar dividir el proceso en muchas partes pequeñas y sumarlas. Esta es la esencia del cálculo integral: la suma de “pequeñas partes” se convierte en una cantidad global. En la práctica, esto se expresa mediante integrales.
Interpretación geométrica
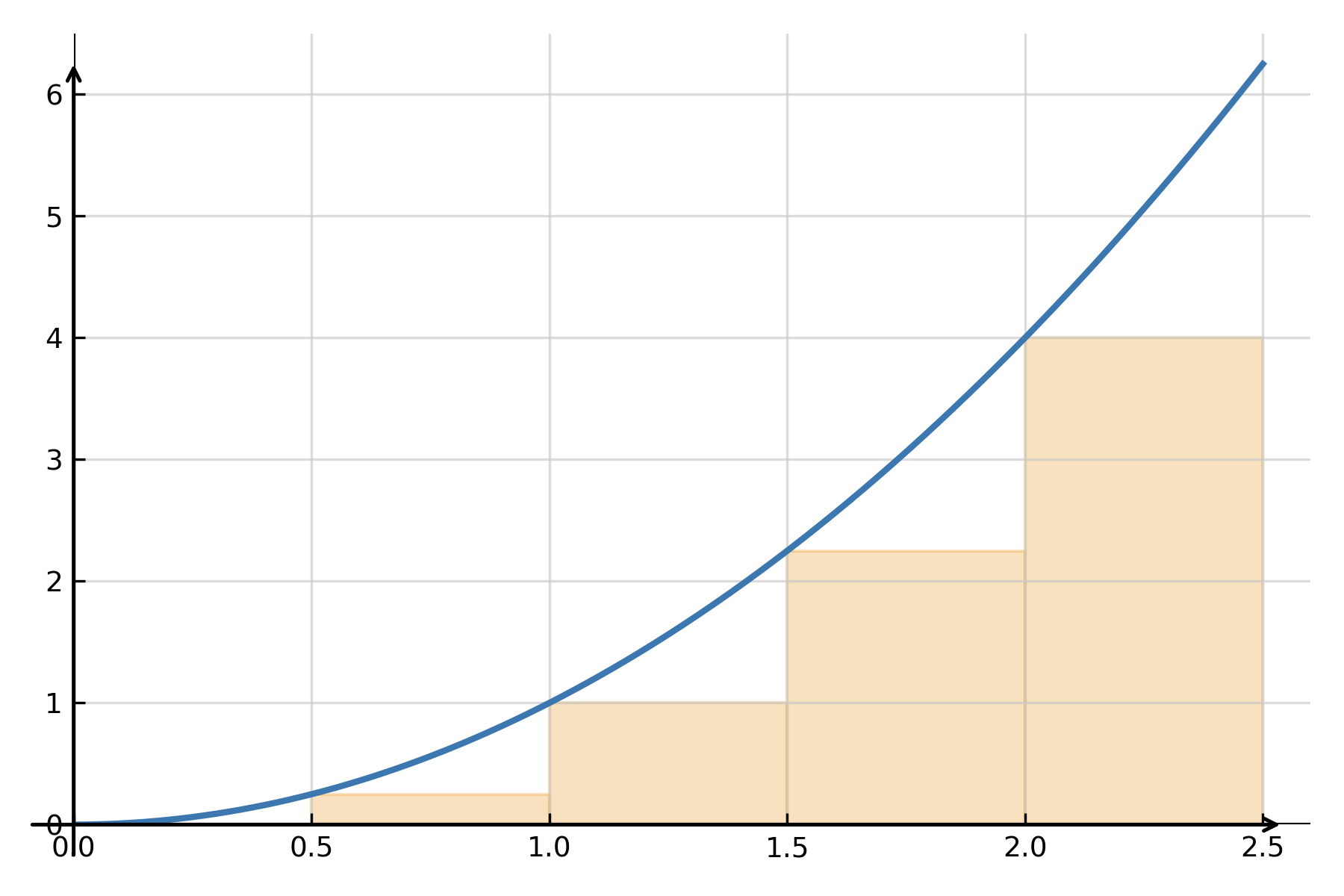
Una interpretación clásica es el área bajo la gráfica de una función no negativa \( \large f(x) \) entre \( \large x=a \) y \( \large x=b \). El área puede aproximarse dividiendo el intervalo en rectángulos estrechos, calculando sus áreas y sumándolas. Cuando el ancho tiende a cero, la suma se aproxima al área exacta.
$$ \large \text{Área} \;=\; \lim_{n \to \infty} \sum_{i=1}^{n} f(x_i)\,\Delta x \;=\; \int_a^b f(x)\,dx $$
El integral proporciona una forma precisa de medir una “cantidad acumulada”, ya sea área, masa, trabajo o cualquier otra cosa.
Integral indefinida (función primitiva)
La integral indefinida representa la “diferenciación inversa”. Si \( \large F'(x)=f(x) \), entonces \( \large F \) se llama una función primitiva de \( \large f \), y se escribe:
$$ \large \int f(x)\,dx \;=\; F(x) + C $$
Aquí \( \large C \) es una constante arbitraria. La integral indefinida representa todas las funciones que tienen la misma derivada \( \large f \).
Integral definida (área y suma)
La integral definida mide la cantidad acumulada entre dos límites \( \large a \) y \( \large b \). Se define como el límite de las sumas de Riemann:
$$ \large \int_a^b f(x)\,dx \;=\; \lim_{n\to\infty}\sum_{i=1}^{n} f(x_i)\,\Delta x $$
Si \( \large f \ge 0 \) en el intervalo, esto representa el área bajo la gráfica. Si \( \large f \) cambia de signo, el área bajo el eje x se cuenta como negativa, reflejando la acumulación neta.
Relación con el cálculo diferencial (Teorema fundamental)
El cálculo integral y el diferencial están vinculados por el teorema fundamental: Si \( \large f \) es continua en \( \large [a,b] \) y \( \large F \) es una función primitiva de \( \large f \), entonces
$$ \large \int_a^b f(x)\,dx \;=\; F(b) - F(a) $$
Esto significa que un área (una suma) puede calcularse usando una función primitiva, y que la diferenciación y la integración son procesos inversos.
Ejemplos
1. Área bajo una función simple
Calcular \( \large \int_0^2 x\,dx \). Una función primitiva es \( \large F(x)=\tfrac{1}{2}x^2 \), por lo tanto:
$$ \large \int_0^2 x\,dx \;=\; \Big[\tfrac{1}{2}x^2\Big]_0^2 \;=\; \tfrac{1}{2}\cdot 4 - 0 \;=\; 2 $$
2. Distancia acumulada a partir de una función de velocidad
Si la velocidad de un coche es \( \large v(t)=3t \) (m/s), la distancia recorrida desde \( \large t=0 \) hasta \( \large t=4 \) es:
$$ \large s \;=\; \int_0^4 v(t)\,dt \;=\; \int_0^4 3t\,dt \;=\; \Big[\tfrac{3}{2}t^2\Big]_0^4 \;=\; 24\ \text{m} $$
Esto muestra que el área bajo la curva de velocidad corresponde a la distancia total recorrida.
Por qué existen dos tipos de integrales
La integral indefinida (función primitiva) es una herramienta para encontrar fórmulas y trabajar algebraicamente, mientras que la integral definida \( \large \text{mide} \) una cantidad concreta en un intervalo. El teorema fundamental permite traducir entre estas dos perspectivas.
Resumen
El cálculo integral consiste en sumar pequeñas contribuciones para formar una cantidad total. Geométricamente, las integrales se interpretan como áreas; físicamente, como masa, trabajo o distancia acumulada. Gracias al teorema fundamental, las integrales definidas pueden calcularse mediante funciones primitivas, haciendo que el cálculo integral sea el proceso “inverso” natural de la diferenciación.