Ley de senos
La ley de senos puede usarse en los casos en que se conoce un par ángulo-lado, es decir, cuando uno de los lados conocidos se encuentra opuesto al ángulo conocido.
Así, si conoces el ángulo \(A\) y los lados \(a\) y \(b\), debes usar la ley de senos.
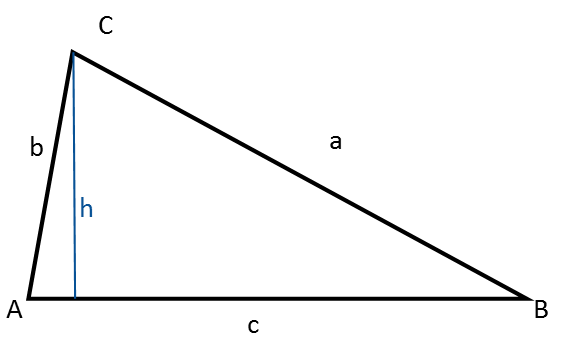
Un triángulo arbitrario no es rectángulo, equilátero ni isósceles.
La ley de senos se expresa de la siguiente manera:
$$ {a \over \sin(A)} = {b \over \sin(B)} = {c \over \sin(C)} $$
Así que si conoces el ángulo \(A\) y los lados \(a\) y \(b\), y necesitas encontrar el ángulo \(B\), usas lo siguiente y aíslas el ángulo \(B\):
$$ {a \over \sin(A)} = {b \over \sin(B)} \Leftrightarrow \\[16pt] \sin(B) = {b \cdot \sin(A) \over a} $$
El resultado será un número entre 0 y 1, por ejemplo 0,866. Para encontrar el ángulo debes usar \( \sin^{-1} \) en tu calculadora:
$$ \sin^{-1}(0,866) = 60^\circ $$
El ángulo es entonces 60 grados.
Si conoces dos ángulos y solo un lado, también puedes usar la ley de senos. Supongamos que conoces los ángulos \(A\) y \(B\), así como el lado \(a\):
$$ {a \over \sin(A)} = {b \over \sin(B)} \Leftrightarrow \\[16pt] b = {a \cdot \sin(B) \over \sin(A)} $$
Nota: Si el cálculo da \(\sin(v) > 1\), no existe solución. Esto significa que el triángulo dado no puede existir con la información que tienes.
Seno y triángulos obtusos
Si calculas ángulos con seno en un triángulo que resulta ser obtuso, debes tener cuidado, porque puede haber dos resultados dependiendo de cuánto sepas del triángulo.
Supongamos que tienes la siguiente información sobre un triángulo:
- Ángulo A = 25 grados
- Lado a = 3
- Lado c = 5
Con esta información podemos calcular el ángulo \(C\):
$$ \begin{align}{a \over \sin(A)} &= {c \over \sin(C)} \Leftrightarrow \\[10pt] \sin(C) &= {c \cdot \sin(A) \over a } \Leftrightarrow \\[10pt] \sin(C) &= {5 \cdot \sin(25^\circ) \over 3 } \Leftrightarrow \\[10pt] \sin(C) &= 0,704 \Leftrightarrow \\[10pt] \sin^{-1}(0,704) &= 44,78^\circ \end{align} $$
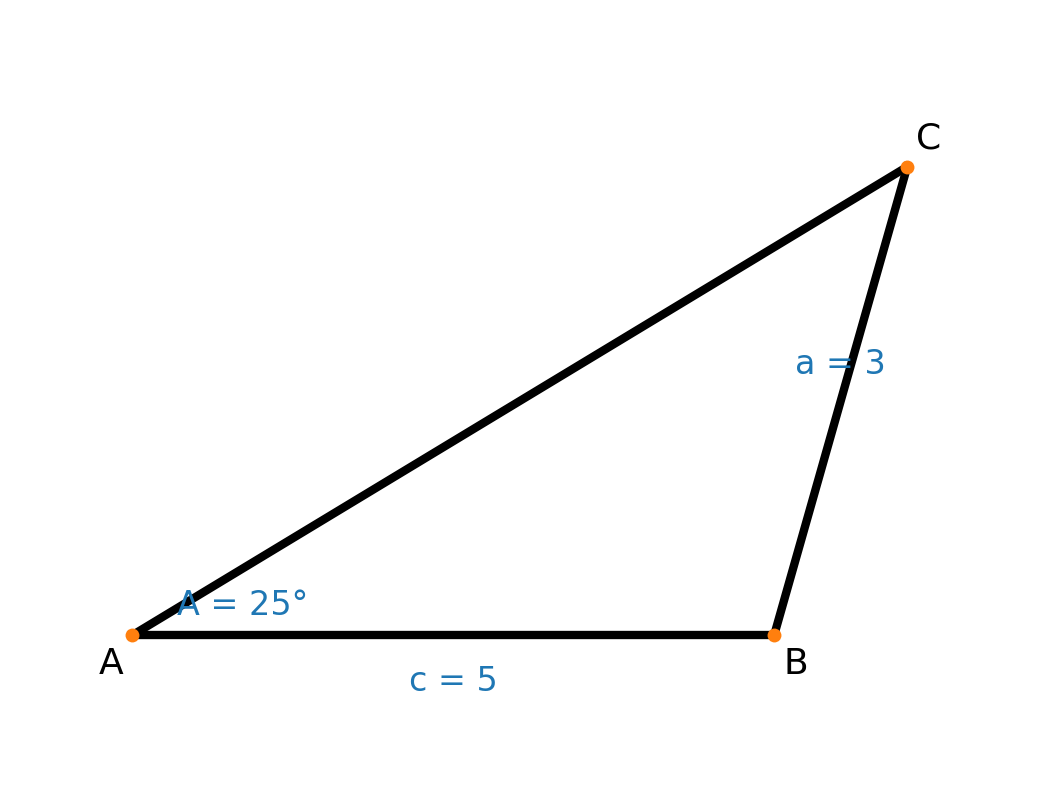
El resultado es por lo tanto un triángulo, como se muestra arriba, con:
- Ángulo A = 25°
- Ángulo B = 110,22°
- Ángulo C = 44,78°
Cálculo del ángulo obtuso
Si miras la figura de abajo, puedes ver que es posible dibujar otro triángulo con la misma información.
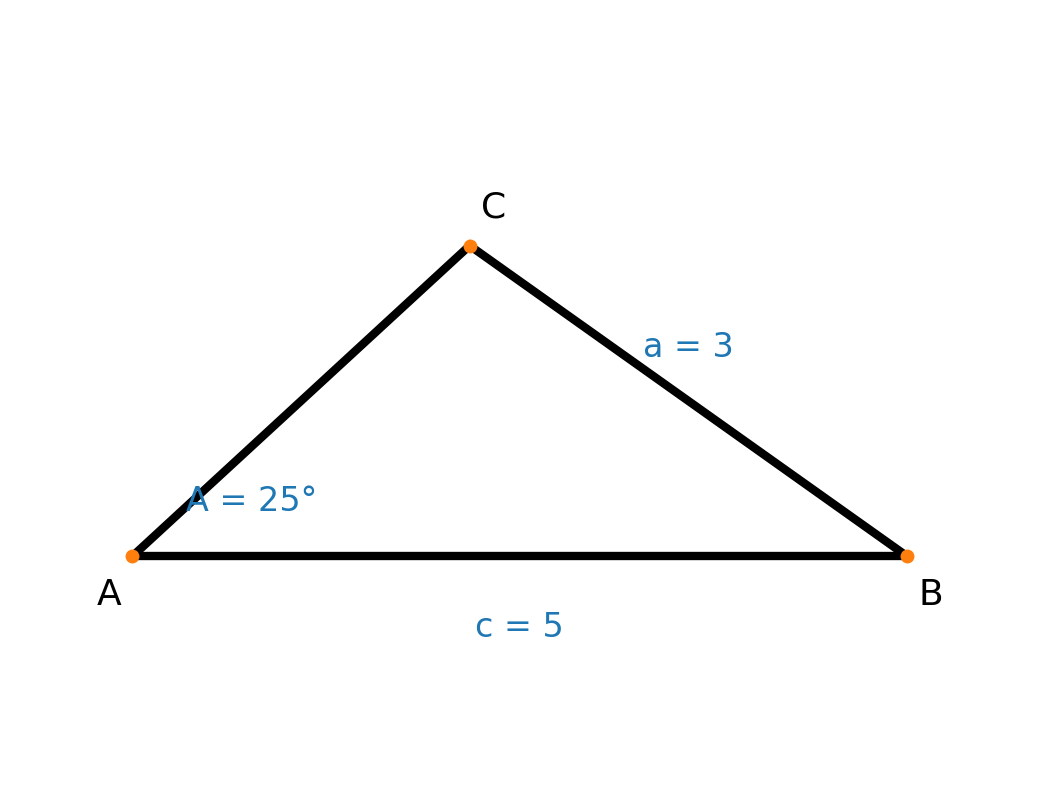
La ley de senos siempre devuelve la solución aguda (entre 0° y 90°). La posible solución obtusa se encuentra restando el ángulo agudo de 180°.
Suponemos que el ángulo agudo es 44,78°, como se calculó anteriormente, y lo llamamos \(C_1\). El ángulo obtuso lo llamamos \(C_2\):
$$ C_2 = 180 - C_1 \Leftrightarrow \\[12pt] C_2 = 135,22^\circ $$
Ahora conoces el ángulo \(C\) para ambos triángulos y puedes calcular el resto para ambos. Esto significa que el lado \(b\) también tiene dos longitudes diferentes (lo mismo ocurre con el perímetro, la altura y el área).
Por lo tanto, siempre debes comprobar si la solución encontrada puede tener un ángulo obtuso al usar la ley de senos.
La regla para saber cuándo hay dos soluciones es: Si el ángulo que calculas con la ley de senos es menor de 90 grados, habrá dos resultados.