Ley de cosenos

La ley de cosenos puede usarse en triángulos arbitrarios, es decir, triángulos que no son rectángulos, isósceles ni equiláteros. Funciona tanto cuando conoces dos lados y el ángulo comprendido como cuando conoces los tres lados.

 

Fórmulas de la ley de cosenos

Si conoces un ángulo y los dos lados que forman el ángulo, puedes encontrar el tercer lado usando la ley de cosenos:

 

$$ a^2 = b^2 + c^2 - 2 \cdot b \cdot c \cdot \cos(A) $$

$$ b^2 = a^2 + c^2 - 2 \cdot a \cdot c \cdot \cos(B) $$

$$ c^2 = a^2 + b^2 - 2 \cdot a \cdot b \cdot \cos(C) $$

 

Nota: si el triángulo es rectángulo, basta con usar el teorema de Pitágoras. La ley de cosenos es especialmente útil para triángulos arbitrarios.

 

Cálculo de ángulos

Si conoces los tres lados de un triángulo, puedes encontrar los ángulos aislando el coseno en la fórmula:

 

$$ \cos(A) = \frac{b^2 + c^2 - a^2}{2 \cdot b \cdot c} $$

$$ \cos(B) = \frac{a^2 + c^2 - b^2}{2 \cdot a \cdot c} $$

$$ \cos(C) = \frac{a^2 + b^2 - c^2}{2 \cdot a \cdot b} $$

 

El resultado será un número entre -1 y 1. Para encontrar el ángulo, usa \( \cos^{-1} \) en tu calculadora:

 

$$ \cos^{-1}(0,866) = 30^\circ $$

 

El ángulo es por lo tanto de 30 grados.

 

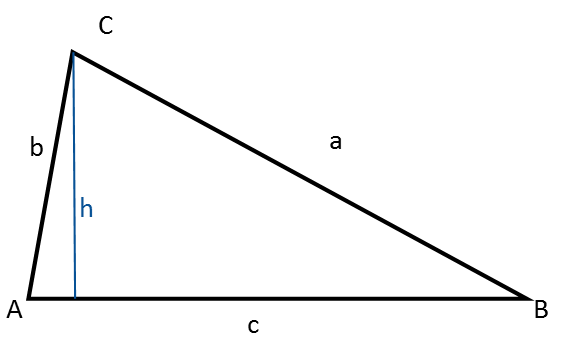
Un triángulo arbitrario no es rectángulo, equilátero ni isósceles.

Observa que la altura lo divide en dos triángulos rectángulos.