Fórmulas de ángulo doble y medio ángulo

En trigonometría, las fórmulas de ángulo doble y medio ángulo describen cómo se pueden expresar el seno, el coseno y la tangente cuando el ángulo se duplica o se reduce a la mitad.

Las fórmulas se derivan directamente de las fórmulas de adición y sustracción y permiten encontrar nuevas relaciones entre las funciones trigonométricas.

 

Fórmulas de ángulo doble

Al poner \( \alpha = \beta \) en las fórmulas de adición obtenemos:

 

$$ \large \sin(2v) = 2 \sin(v) \cdot \cos(v) $$

$$ \large \cos(2v) = \cos^2(v) - \sin^2(v) $$

$$ \large \tan(2v) = \frac{2 \tan(v)}{1 - \tan^2(v)} $$

 

 

 

La fórmula del coseno también puede reescribirse en otras formas útiles utilizando la identidad pitagórica:

 

$$ \large \cos(2v) = 2\cos^2(v) - 1 = 1 - 2\sin^2(v) $$

 

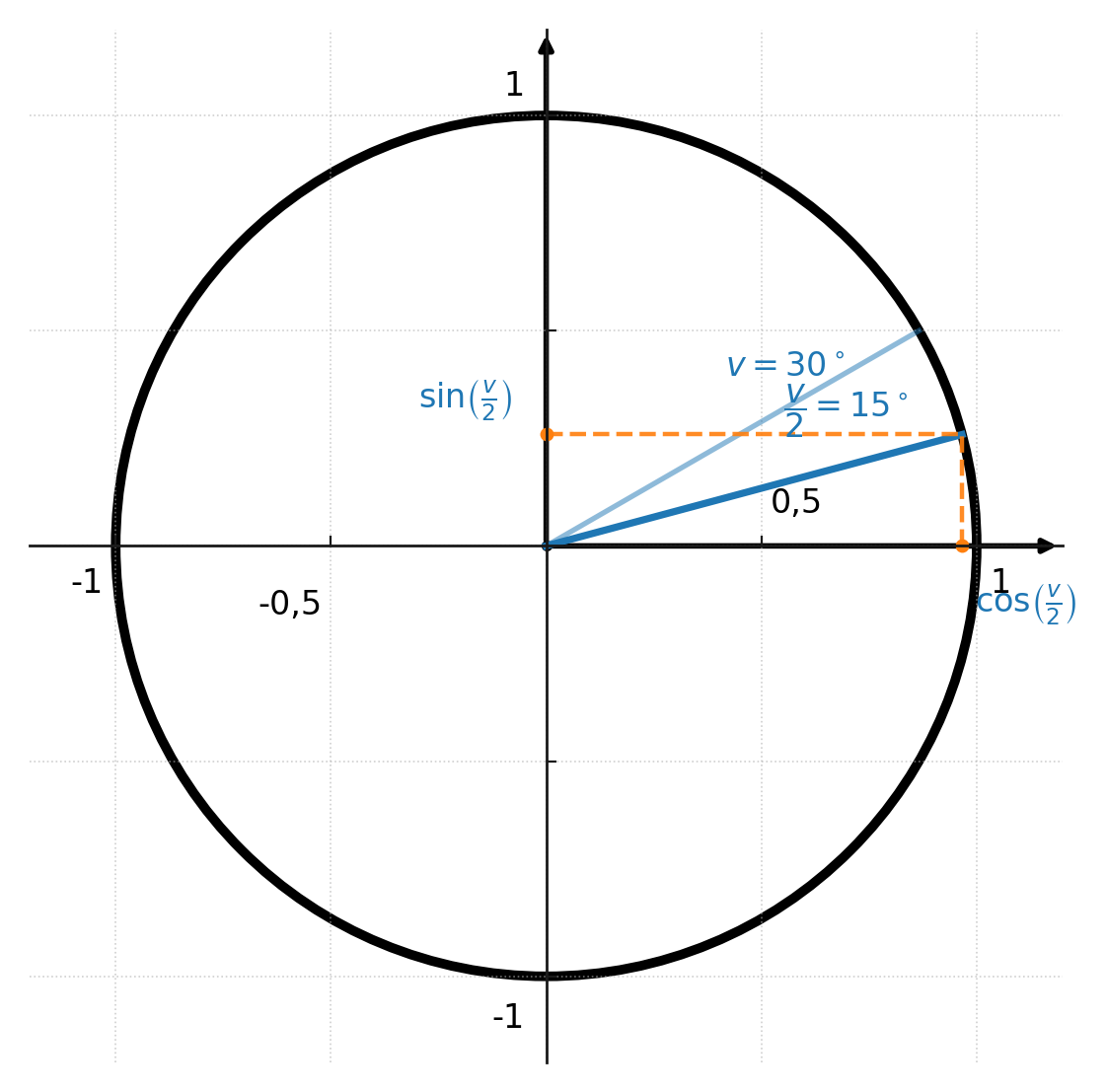
Fórmulas de medio ángulo

Las fórmulas de medio ángulo se obtienen aislando \(\sin v\) y \(\cos v\) en las fórmulas de ángulo doble. El resultado es:

 

$$ \large \sin\!\left(\tfrac{v}{2}\right) = \pm \sqrt{\tfrac{1 - \cos(v)}{2}} $$

$$ \large \cos\!\left(\tfrac{v}{2}\right) = \pm \sqrt{\tfrac{1 + \cos(v)}{2}} $$

$$ \large \tan\!\left(\tfrac{v}{2}\right) = \tfrac{\sin(v)}{1 + \cos(v)} = \tfrac{1 - \cos(v)}{\sin(v)} $$

 

Los signos \(+\) o \(-\) dependen de en qué cuadrante se encuentre el ángulo.

 

 

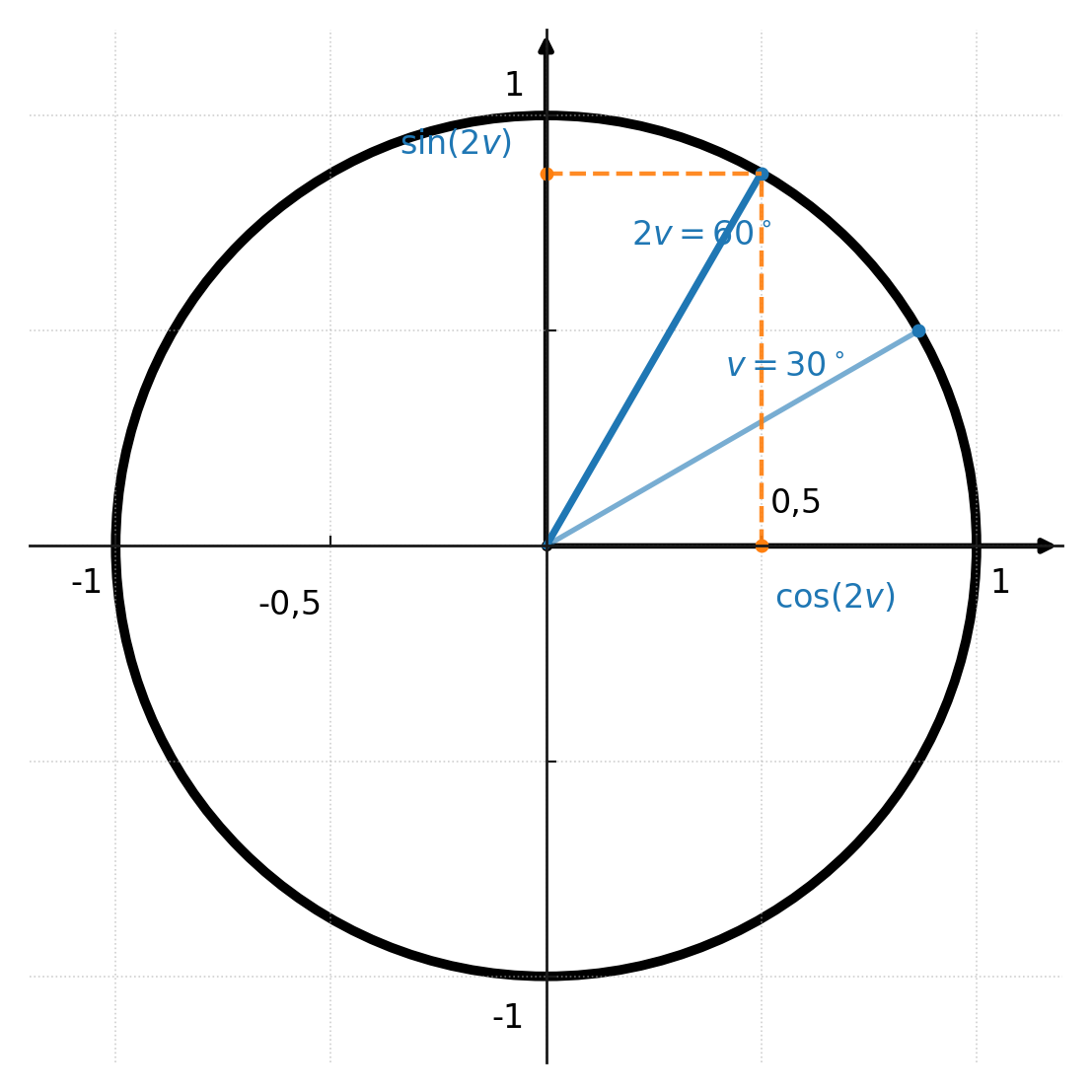
Ejemplo

Queremos calcular \( \sin(2 \cdot 30^\circ) \):

 

$$ \large \sin(60^\circ) = 2 \cdot \sin(30^\circ) \cdot \cos(30^\circ) $$

$$ \large = 2 \cdot \tfrac{1}{2} \cdot \tfrac{\sqrt{3}}{2} = \tfrac{\sqrt{3}}{2} $$

 

Aplicación

• Las fórmulas se utilizan para encontrar valores exactos de ángulos como 15°, 22,5° y 75°.
• Son útiles en demostraciones y transformaciones trigonométricas.
• Las fórmulas de medio ángulo se utilizan a menudo para resolver ecuaciones trigonométricas.