Adición y sustracción de ángulos
En trigonometría, la adición y sustracción de ángulos describe las fórmulas que muestran cómo cambian el seno, el coseno y la tangente cuando se suman o se restan dos ángulos.
Las fórmulas permiten calcular valores de nuevos ángulos a partir de ángulos conocidos.
Por ejemplo, se puede calcular cos(75°), aunque no aparezca en las tablas, usando cos(45° + 30°).
Fórmulas de adición y sustracción
Coseno:
$$ \large \cos(\alpha + \beta) = \cos(\alpha) \cdot \cos(\beta) - \sin(\alpha) \cdot \sin(\beta) $$
$$ \large \cos(\alpha - \beta) = \cos(\alpha) \cdot \cos(\beta) + \sin(\alpha) \cdot \sin(\beta) $$
Seno:
$$ \large \sin(\alpha + \beta) = \sin(\alpha) \cdot \cos(\beta) + \cos(\alpha) \cdot \sin(\beta) $$
$$ \large \sin(\alpha - \beta) = \sin(\alpha) \cdot \cos(\beta) - \cos(\alpha) \cdot \sin(\beta) $$
Tangente:
$$ \large \tan(\alpha + \beta) = \frac{\tan(\alpha) + \tan(\beta)}{1 - \tan(\alpha) \cdot \tan(\beta)} $$
$$ \large \tan(\alpha - \beta) = \frac{\tan(\alpha) - \tan(\beta)}{1 + \tan(\alpha) \cdot \tan(\beta)} $$
Ejemplo
Queremos calcular \( \cos(75^\circ) \). Se puede escribir como \( \cos(45^\circ + 30^\circ) \):
$$ \large \cos(75^\circ) = \cos(45^\circ + 30^\circ) $$
$$ \large = \cos(45^\circ) \cdot \cos(30^\circ) - \sin(45^\circ) \cdot \sin(30^\circ) $$
$$ \large = \tfrac{\sqrt{2}}{2} \cdot \tfrac{\sqrt{3}}{2} - \tfrac{\sqrt{2}}{2} \cdot \tfrac{1}{2} $$
$$ \large = \tfrac{\sqrt{6}}{4} - \tfrac{\sqrt{2}}{4} = \tfrac{\sqrt{6} - \sqrt{2}}{4} $$
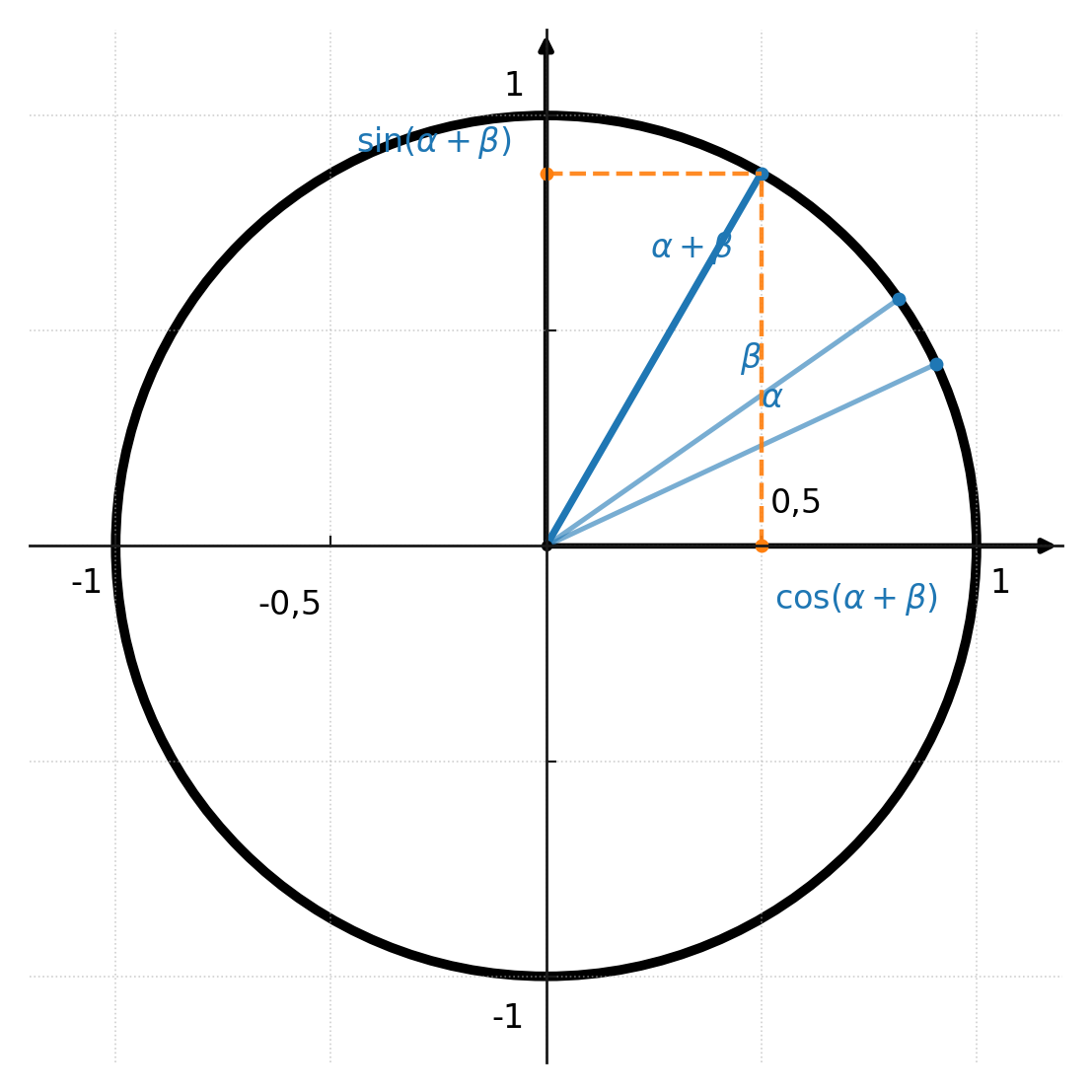
Las fórmulas también pueden entenderse geométricamente a partir del círculo unitario.
Aplicaciones
- Se pueden calcular valores exactos para ángulos como 15°, 75° y 105°.
- Las fórmulas son la base de las fórmulas del ángulo doble y del ángulo mitad (poniendo \( \alpha = \beta \)).
- Se utilizan en demostraciones e identidades en trigonometría avanzada y análisis.