Relaciones

En trigonometría, las relaciones son las fórmulas y conexiones que vinculan entre sí las funciones trigonométricas. Mientras que las funciones (seno, coseno, tangente, etc.) describen cada una una razón específica, las relaciones muestran cómo se conectan las funciones y cómo pueden usarse para calcular lados y ángulos en triángulos.

 

Identidad pitagórica

Una de las relaciones más fundamentales es la identidad pitagórica, que muestra la conexión entre seno y coseno para cualquier ángulo:

 

$$ \sin^2(v) + \cos^2(v) = 1 $$

 

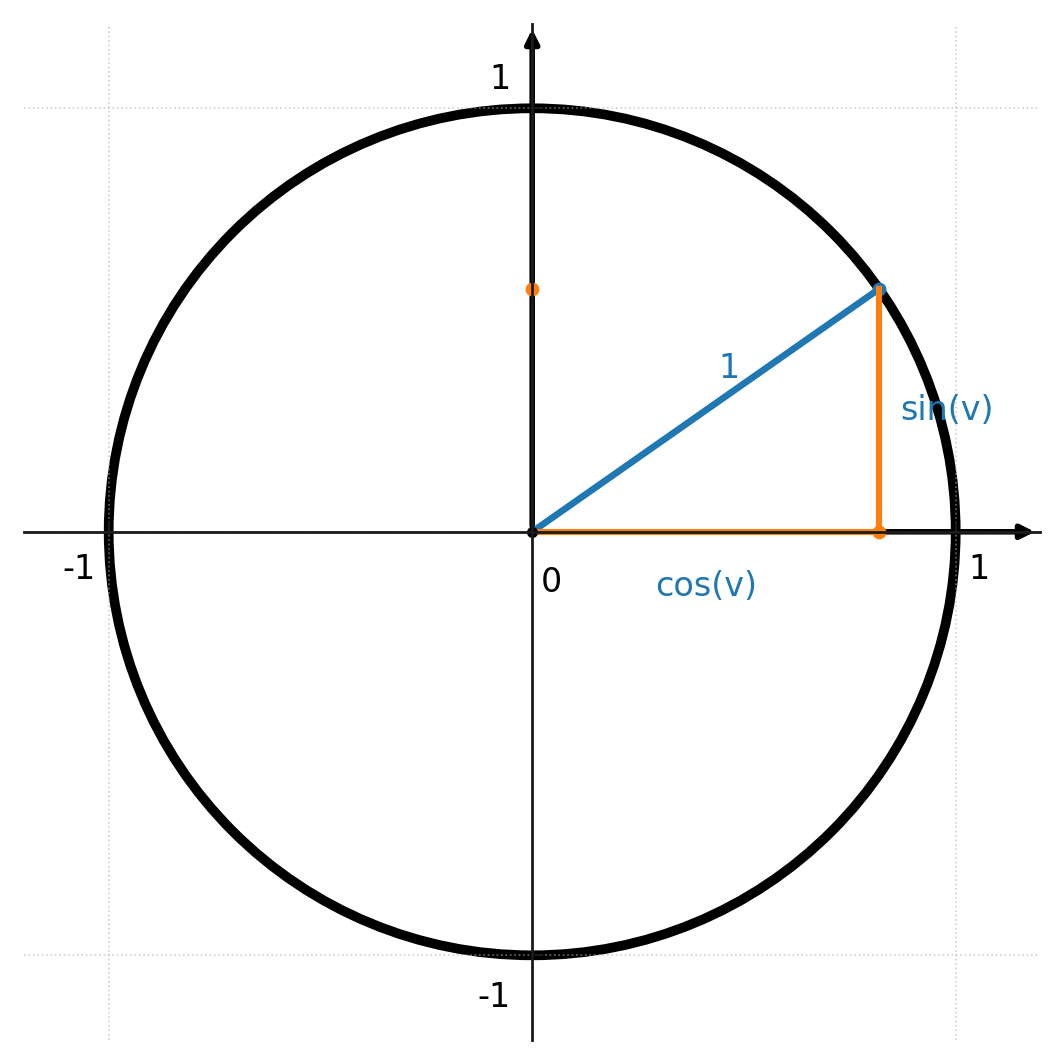
La identidad se deriva directamente del círculo unitario.

Si un punto en el círculo tiene las coordenadas \( (\cos v, \sin v) \), se cumple el teorema de Pitágoras, porque el radio siempre es 1:

 

$$ (\cos v)^2 + (\sin v)^2 = 1^2 = 1 $$

 

 

Aplicación

La identidad pitagórica permite calcular el seno si se conoce el coseno, o el coseno si se conoce el seno.

También es la base de muchas otras identidades trigonométricas.

 

Ejemplo: Si \( \cos v = 0.6 \), el seno se puede calcular así:

 

$$ \sin^2(v) = 1 - \cos^2(v) = 1 - 0.6^2 = 0.64 $$

$$ \sin(v) = \pm \sqrt{0.64} = \pm 0.8 $$

 

Observa que hay dos soluciones, porque el ángulo puede estar tanto en el primer como en el segundo cuadrante.

 

La identidad pitagórica es la relación trigonométrica más fundamental y constituye la base de muchas otras fórmulas y cálculos en trigonometría.