Variance and standard deviation
Dispersion
Dispersion tells how much the observations vary around the mean.
If all observations are close to the mean, the dispersion is small. If they are far from the mean, the dispersion is large.
Variance
The variance measures the average squared distance from the mean.
To find the variance you must:
- Subtract the mean from each observation
- Square the differences
- Find the average of the squared differences
$$ s^2 = \frac{(x_1 - \overline{x})^2 + (x_2 - \overline{x})^2 + ... + (x_n - \overline{x})^2}{n} $$
Standard deviation
The standard deviation is the square root of the variance. It tells, in the same unit as the observations, how much they typically deviate from the mean.
$$ s = \sqrt{s^2} $$
Example
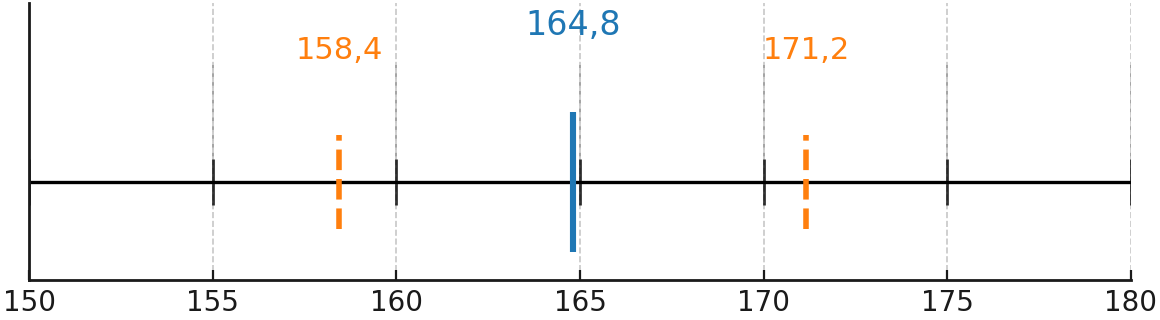
We use the observation of the students’ heights.
- The mean is \( \overline{x} = 164{,}8 \)
- The variance is \( s^2 = 40{,}36 \)
- The standard deviation is \( s \approx 6{,}35 \)
This means that the heights deviate on average about 6.35 cm from the mean.
Diagram
The standard deviation can be shown in a diagram, where the mean is marked and the intervals \( \overline{x} \pm s \) are displayed.