Vektortypen und Rollen

Vektoren können je nach Zusammenhang unterschiedliche Rollen haben. Einige dienen zur Beschreibung von Richtungen, andere zur Angabe einer senkrechten Richtung oder als Grundlage für ein ganzes Koordinatensystem. Hier betrachten wir die wichtigsten Vektortypen.

 

 

Richtungsvektoren

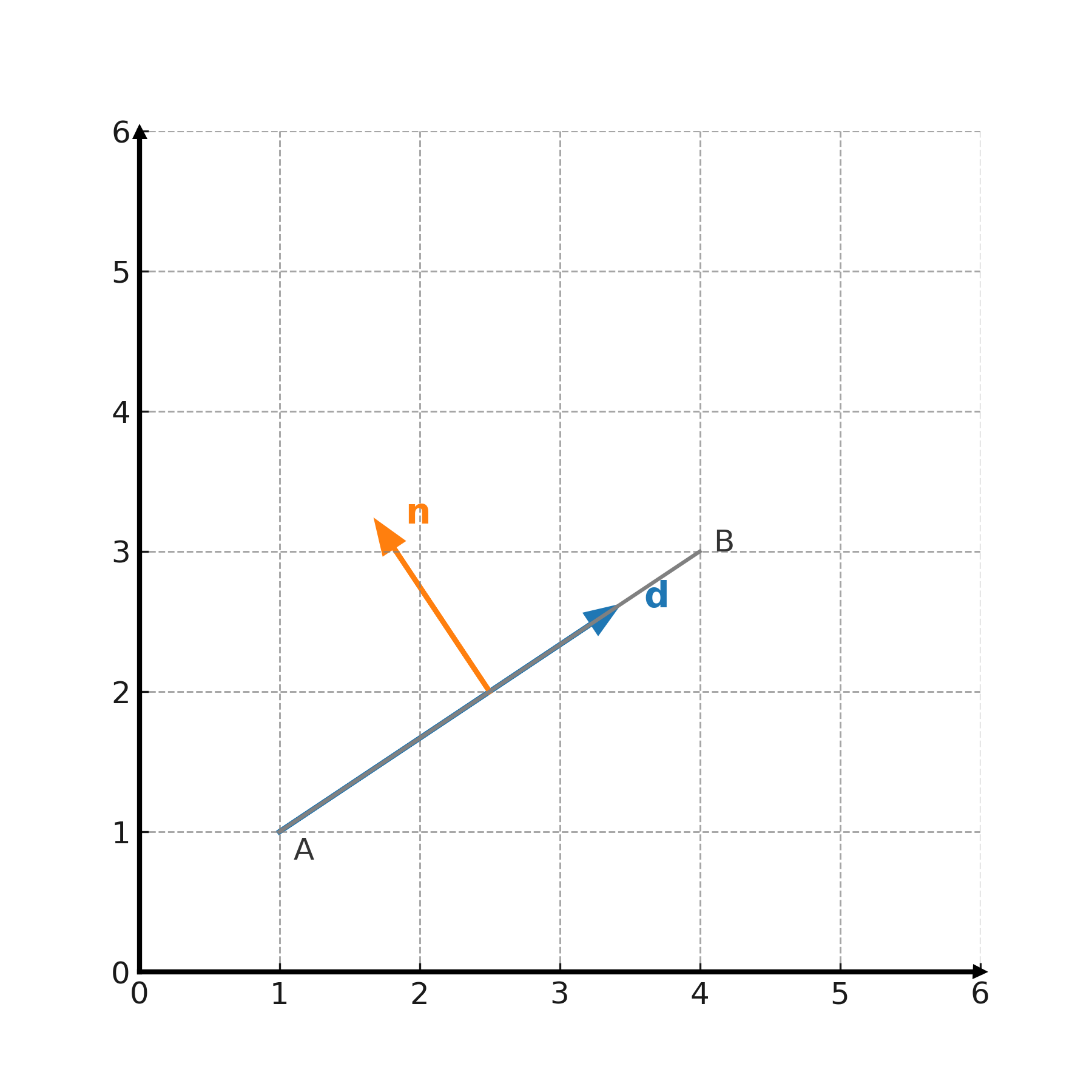
Ein Richtungsvektor (d) beschreibt die Richtung einer Geraden oder einer Ebene. Wenn eine Gerade durch die Punkte \( \large A=(x_1,y_1) \) und \( \large B=(x_2,y_2) \) verläuft, dann ist

 

$$ \large \mathbf{d} = (x_2-x_1,\; y_2-y_1) $$

 

ein Richtungsvektor der Geraden. Mit einem Richtungsvektor kann man eine Parameterdarstellung schreiben:

 

$$ \large (x,y) = (x_1,y_1) + t \cdot \mathbf{d}, \quad t \in \mathbb{R} $$

 

die alle Punkte der Geraden beschreibt.

 

 

Normalvektoren

Ein Normalvektor steht senkrecht auf einer Geraden oder einer Ebene. Hat die Gerade den Richtungsvektor \( \large (a,b) \), dann sind

 

$$ \large \mathbf{n} = (-b,a) \quad \text{oder} \quad (b,-a) $$

 

Normalvektoren. Ein Normalvektor kann verwendet werden, um eine Gerade in der Form

 

$$ \large n_1 \cdot x + n_2 \cdot y + c = 0 $$

 

zu schreiben, wobei \( \large (n_1,n_2) \) der Normalvektor ist. Dass ein Vektor normal ist, kann mit dem Skalarprodukt getestet werden: Wenn \( \large \mathbf{r} \cdot \mathbf{n} = 0 \), dann stehen sie senkrecht aufeinander.

 

 

Einheitsvektoren

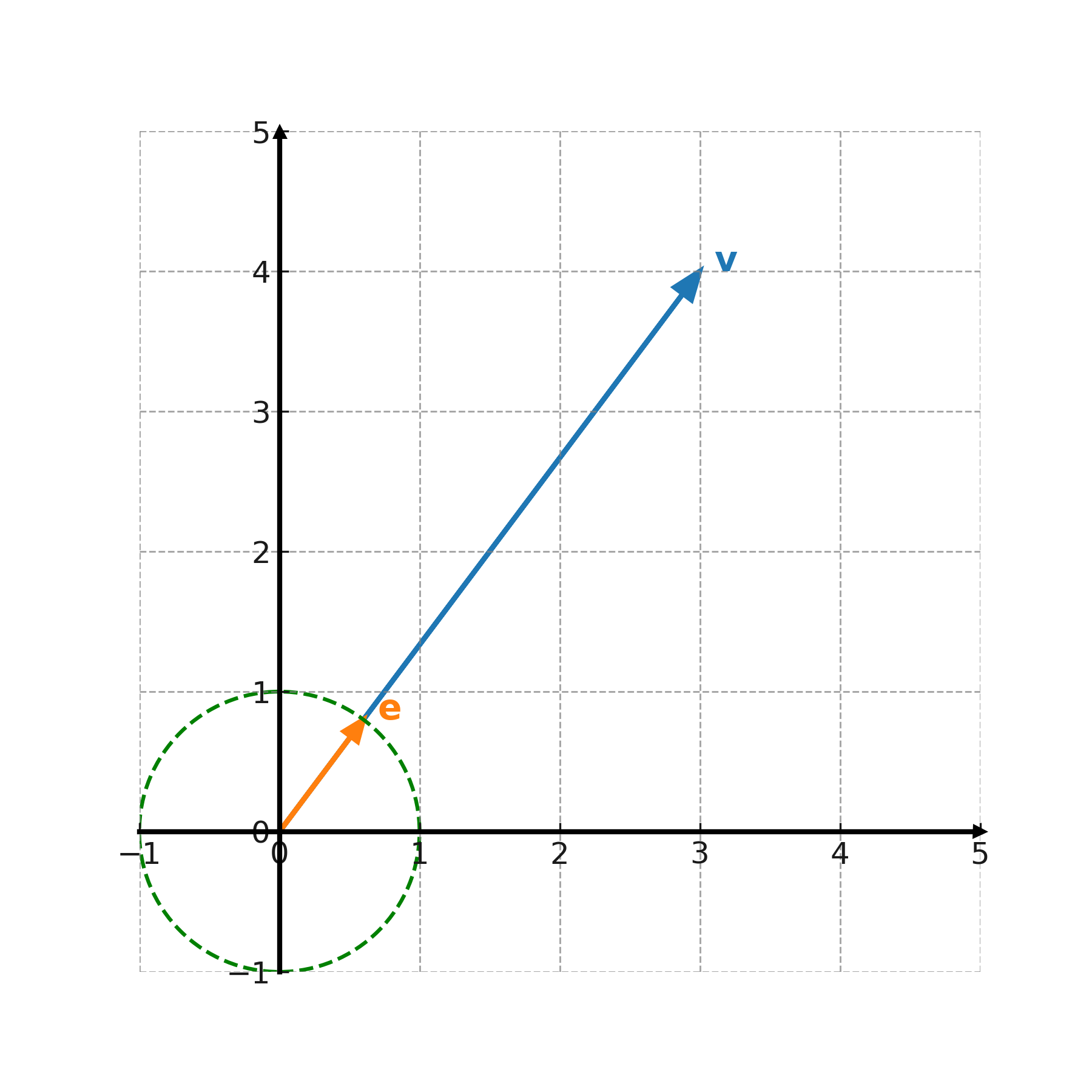
Ein Einheitsvektor hat die Länge 1 und wird verwendet, um eine reine Richtung zu beschreiben. Jeder Vektor kann zu einem Einheitsvektor gemacht werden, indem man ihn durch seine Länge teilt:

 

$$ \large \mathbf{e} = \frac{1}{|\mathbf{v}|} \cdot \mathbf{v} $$

 

Einheitsvektoren werden zum Beispiel verwendet, um die Richtungen der Achsen in einem Koordinatensystem zu definieren.

 

 

Tangentenvektoren

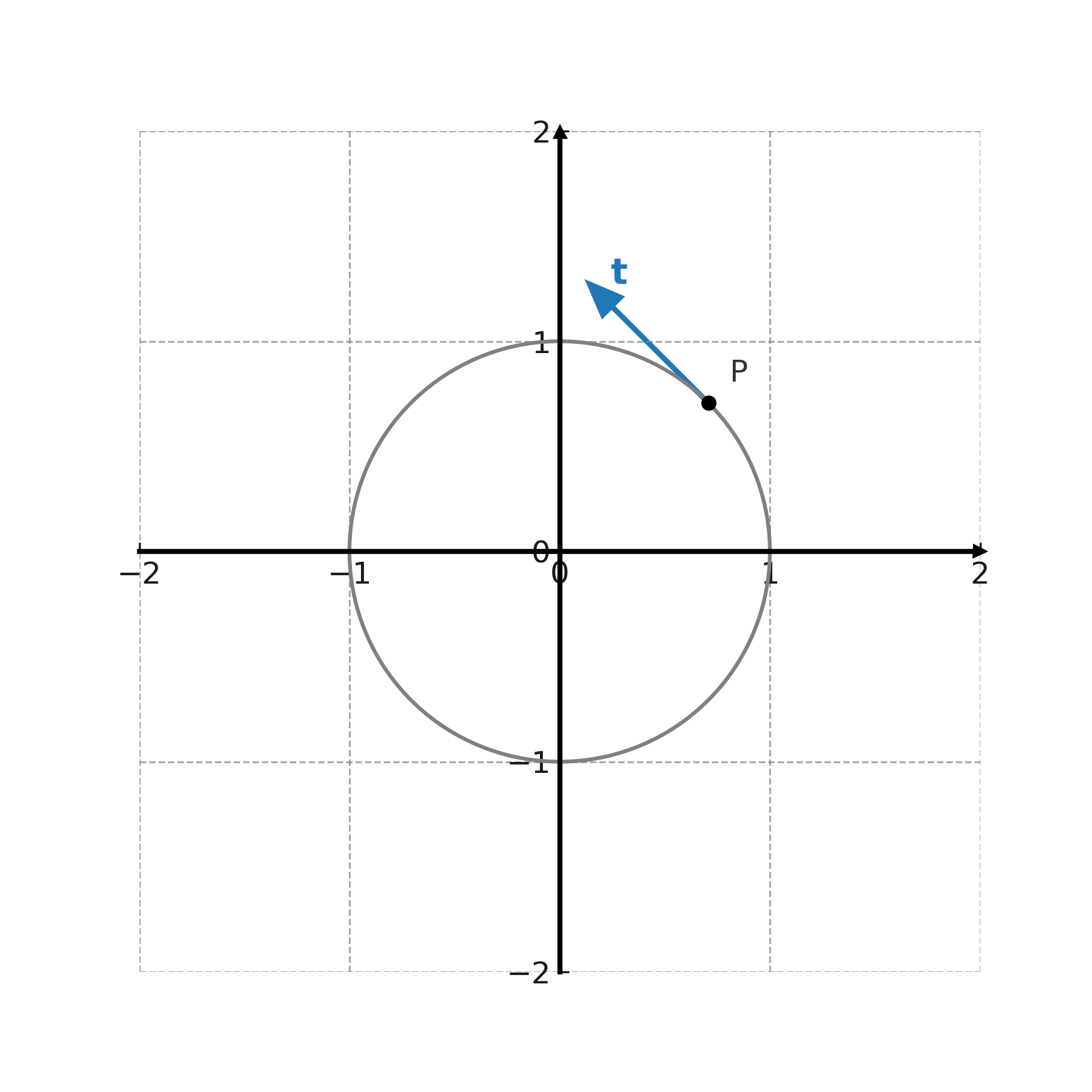
Im Zusammenhang mit Kurven werden Tangentenvektoren verwendet, um die Richtung in einem bestimmten Punkt zu beschreiben. Für eine differenzierbare Kurve \( \large (x(t),y(t)) \) ist der Tangentenvektor gegeben durch

 

$$ \large \mathbf{t} = \big(x'(t),\,y'(t)\big) $$

 

was zeigt, wie sich die Kurve im Punkt bewegt.

 

Basisvektoren

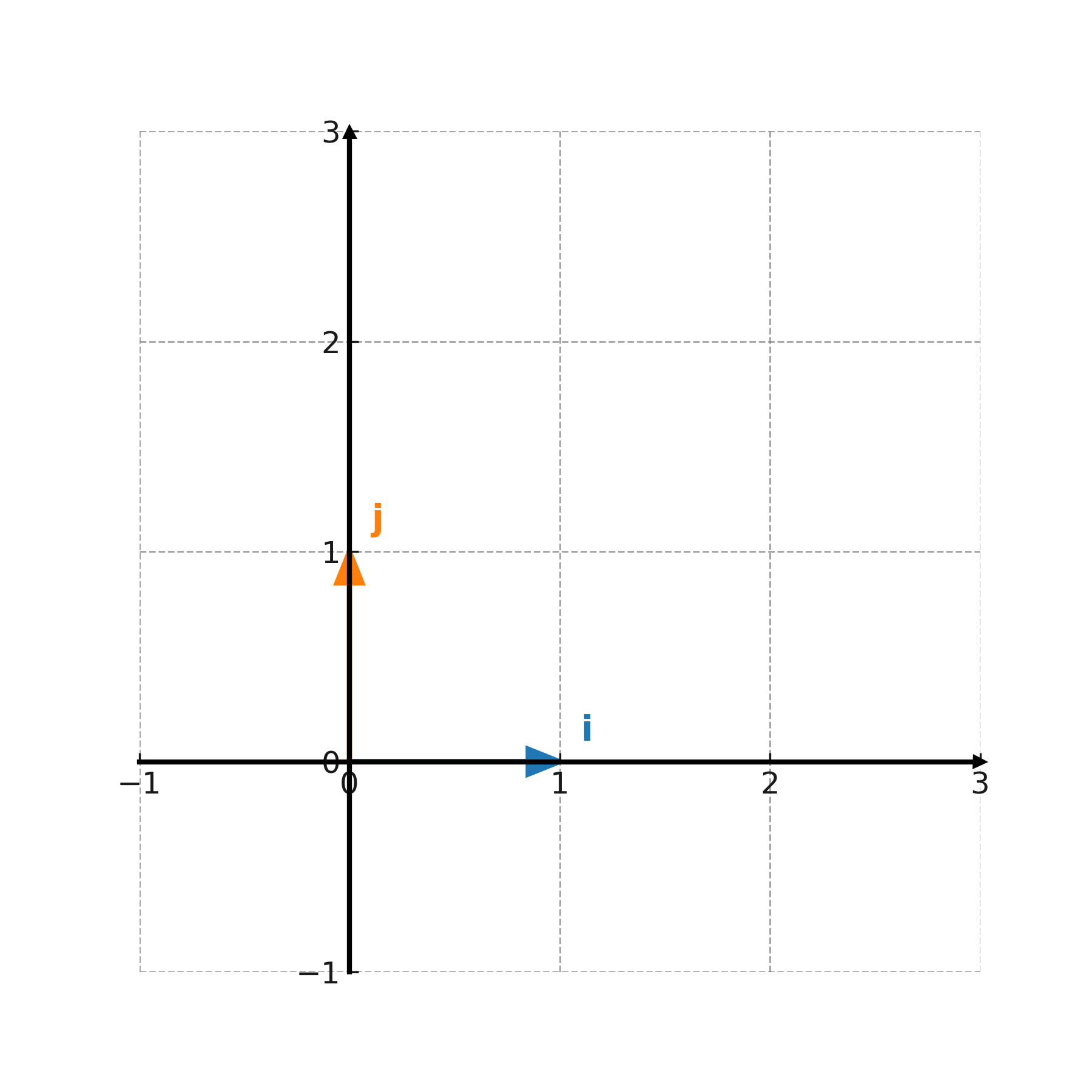
In einem Koordinatensystem werden Basisvektoren verwendet, um alle anderen Vektoren zu beschreiben. In der Ebene ist die Standardbasis

 

$$ \large \mathbf{i} = (1,0), \quad \mathbf{j} = (0,1) $$

 

Jeder Vektor kann als Kombination dieser geschrieben werden: \( \large \mathbf{v} = x \cdot \mathbf{i} + y \cdot \mathbf{j} \).

 

Zusammenfassung

Richtungsvektoren werden verwendet, um Richtungen von Geraden und Ebenen anzugeben, Normalvektoren zur Angabe senkrechter Richtungen, Einheitsvektoren zur Isolierung der reinen Richtung, Tangentenvektoren zur Beschreibung des Verlaufs von Kurven und Basisvektoren zum Aufbau ganzer Koordinatensysteme. Zusammen bilden sie die Grundlage für die Anwendung von Vektoren in Geometrie und Algebra.