Ein Trapez ist ein Viereck, bei dem zwei Seiten parallel sind. Die parallelen Seiten werden Grundseiten genannt.

Wenn auch die anderen beiden Seiten parallel sind, ist die Figur ein Parallelogramm. Die nicht parallelen Seiten werden Schenkel genannt.

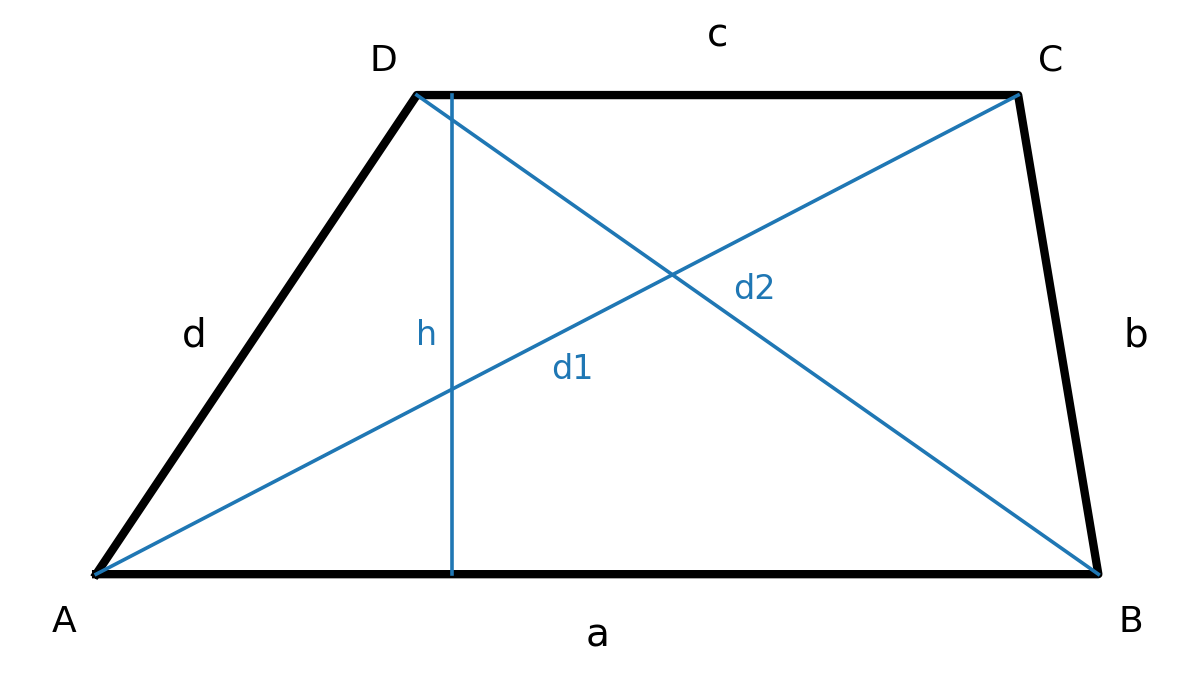
Varianten

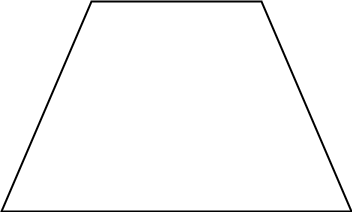
Gleichschenkliges Trapez: \(b=d\). Die Basiswinkel an jeder Grundseite sind paarweise gleich groß, und die Diagonalen sind gleich lang.

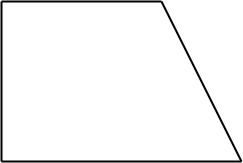
Rechtwinkliges Trapez: Zwei der Winkel sind rechte Winkel.

Eigenschaften

• Die Summe der Innenwinkel beträgt 360°.
• Entlang jedes Schenkels gilt \( \angle A + \angle D = 180^\circ \) und \( \angle B + \angle C = 180^\circ \) (Parallelität).
• Die Mittellinie (die Linie zwischen den Mittelpunkten der Schenkel) hat die Länge \( m=\tfrac{a+c}{2} \), und die Fläche kann geschrieben werden als \( A=m\cdot h \).

Fläche und Umfang

Die Standardformel für die Fläche:

$$ \large A=\tfrac{h}{2}\,(a+c) $$

Wenn die Basiswinkel bei \(A\) und \(B\) bekannt sind, können die Schenkellängen geschrieben werden als \( d=\tfrac{h}{\sin(\angle A)} \) und \( b=\tfrac{h}{\sin(\angle B)} \). Damit wird der Umfang:

$$ \large P = (a+c) + h\!\left(\tfrac{1}{\sin(\angle A)}+\tfrac{1}{\sin(\angle B)}\right) $$

Fläche aus vier Seiten

Sind alle vier Seiten bekannt, kann die Höhe und damit die Fläche ohne Winkel berechnet werden:

$$ \large A = \tfrac{1}{2}(a+c)\,\sqrt{\,b^2 - \Bigl(\tfrac{(a-c)^2 + b^2 - d^2}{2(a-c)}\Bigr)^2} $$

Hier wird \(a \ne c\) vorausgesetzt. Für ein Parallelogramm nimmt man den Grenzwert \(a \to c\).

Diagonalen

Die Diagonalen erhält man mit dem Kosinussatz in den zugehörigen Dreiecken:

$$ \large d_1 = \sqrt{a^2 + b^2 - 2ab\cos(\angle B)} $$

$$ \large d_1 = \sqrt{c^2 + d^2 - 2cd\cos(\angle D)} $$

$$ \large d_2 = \sqrt{a^2 + d^2 - 2ad\cos(\angle A)} $$

$$ \large d_2 = \sqrt{b^2 + c^2 - 2bc\cos(\angle C)} $$

In einem gleichschenkligen Trapez gilt \(d_1=d_2\).

Umkreis

Nur gleichschenklige Trapeze können in einen Kreis eingeschrieben werden. Äquivalent gilt für die gegenüberliegenden Winkelsummen:

• \(\angle A + \angle C = 180^\circ\)
• \(\angle B + \angle D = 180^\circ\)

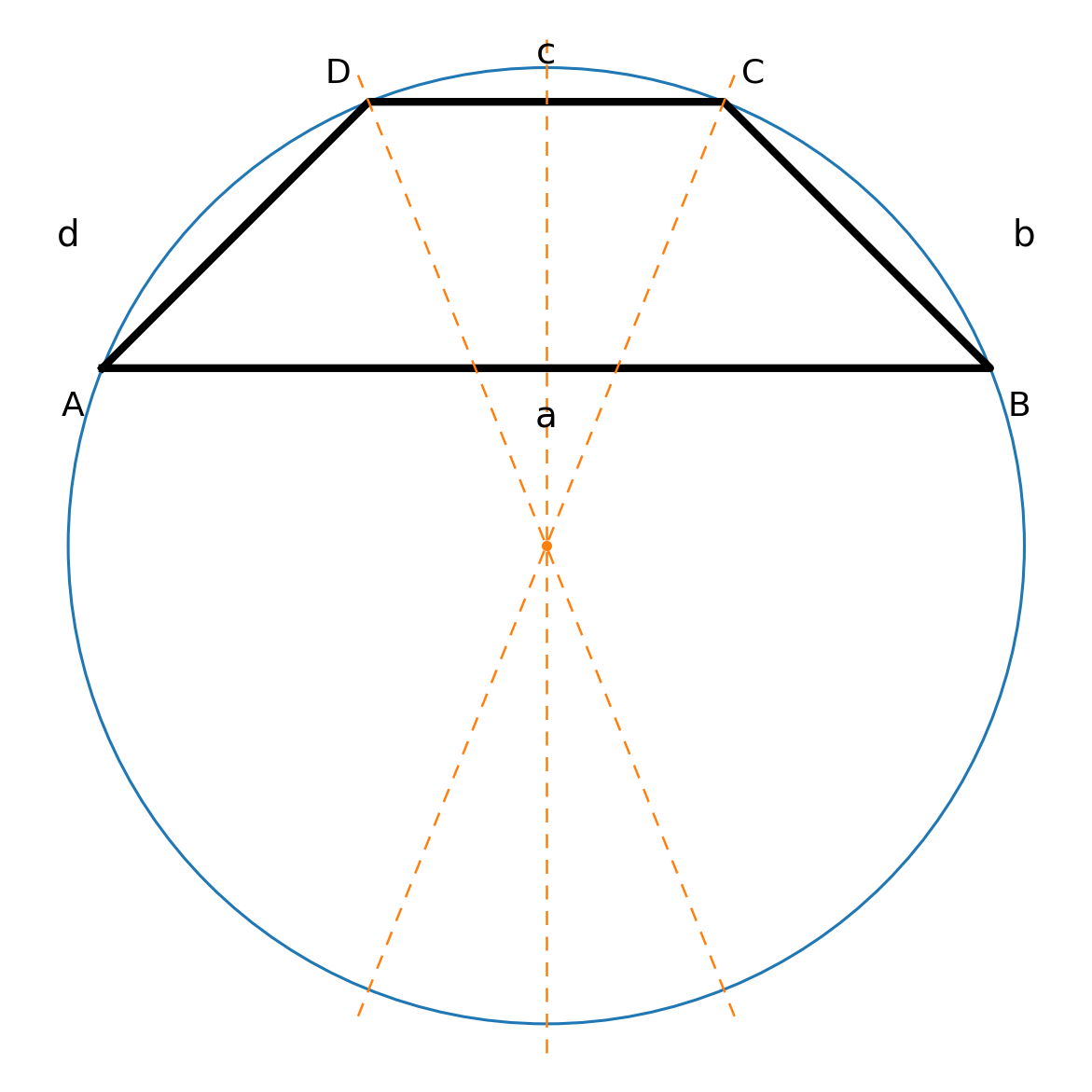
Das Zentrum des Kreises kann gefunden werden, indem man die Winkelhalbierenden von Winkel C und D zeichnet und eventuell auch die Mittelsenkrechte der Seiten a und c (Symmetrieachse).

Beachte, dass für jedes Trapez \( \angle A + \angle D = 180^\circ \) und \( \angle B + \angle C = 180^\circ \) gilt, da die Linien parallel sind. Das macht es nicht von selbst zyklisch.

Inkreis

Ein Trapez hat einen Inkreis, der alle vier Seiten berührt, genau dann wenn gilt:

$$ \large a + c = b + d $$

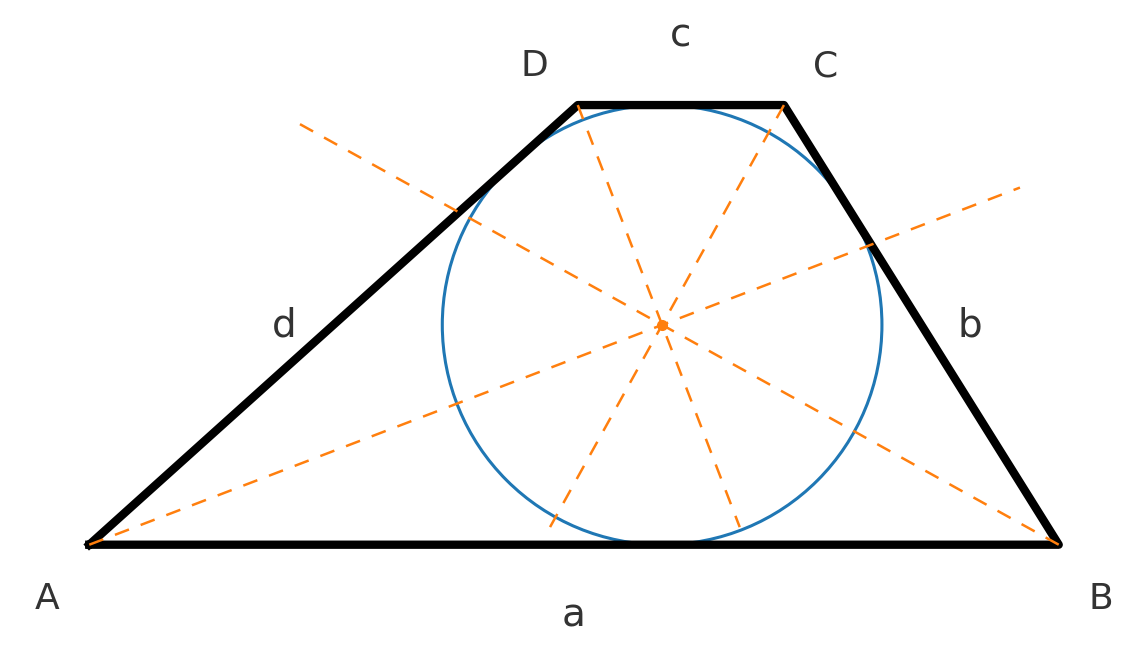
Das Zentrum des Kreises kann gefunden werden, indem man die Winkelhalbierenden aller vier Winkel zeichnet.

Für tangentiale Vierecke gilt außerdem \( A = r \cdot s \), wobei \( r \) der Inkreisradius und \( s \) der Halb­umfang ist.

Anwendungen

• Die Zerlegung in zwei rechtwinklige Dreiecke plus ein Rechteck macht Konstruktionen und trigonometrische Berechnungen übersichtlich.
• Die Trapezregel wird zur numerischen Approximation von Integralen verwendet.