Quadrat und Rechteck
Wenn man Viereck sagt, denken die meisten wohl zuerst an ein Quadrat oder ein Rechteck. Diese beiden rechtwinkligen Figuren sieht man überall.
Es ist dein Computerbildschirm, ein Fußballfeld, ein A4-Blatt Papier usw.
Gemeinsam für alle Vierecke ist, dass die Winkelsumme \(360^\circ\) beträgt
$$ \Large \angle A + \angle B + \angle C + \angle D = 360^\circ $$
Rechteck
Ein Rechteck ist ein Viereck, bei dem alle Winkel 90 Grad betragen. Das bedeutet, dass die Seiten parallel sind.

Quadrat
Wenn alle vier Seiten gleich lang sind, nennt man es ein Quadrat. Ein Quadrat ist also auch ein Rechteck, und deshalb gelten die gleichen Rechenregeln.

Berechnung
Bei einem Rechteck ist es normalerweise notwendig, beide Seiten zu kennen, um Umfang und Fläche zu berechnen. Es sei denn, es ist ein Quadrat, dann reicht eine Seite, da sie gleich sind.
Aber wenn man die Diagonale kennt, kann man das Viereck in zwei rechtwinklige Dreiecke teilen, was andere Berechnungen ermöglicht.
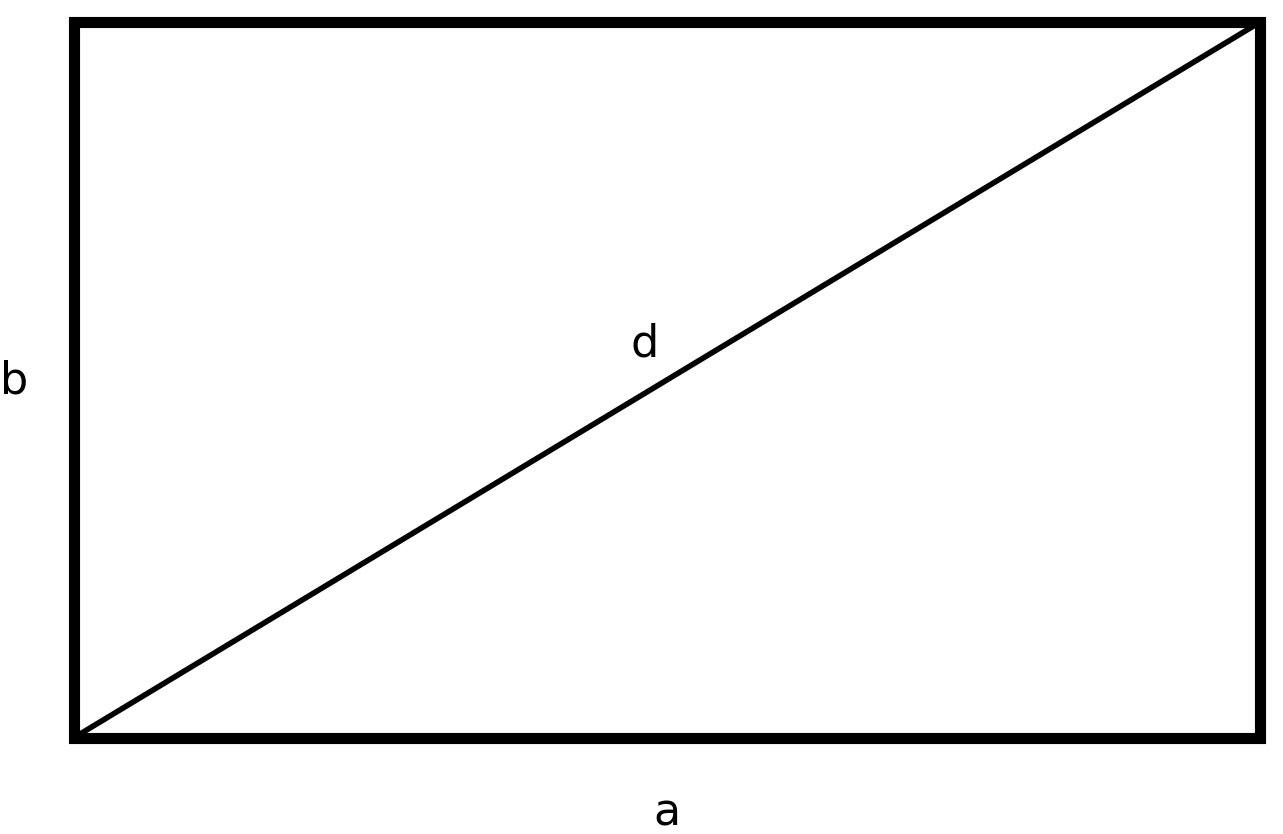
Wenn du Gleichungen gelernt hast, kannst du die Formeln umstellen und die Seiten berechnen, vorausgesetzt, du kennst Fläche oder Umfang.