Parallelogramm

Ein Parallelogramm ist ein Viereck, bei dem die gegenüberliegenden Seiten gleich lang und parallel sind.

Die Figur kann als ein "schiefes Rechteck" betrachtet werden.

 

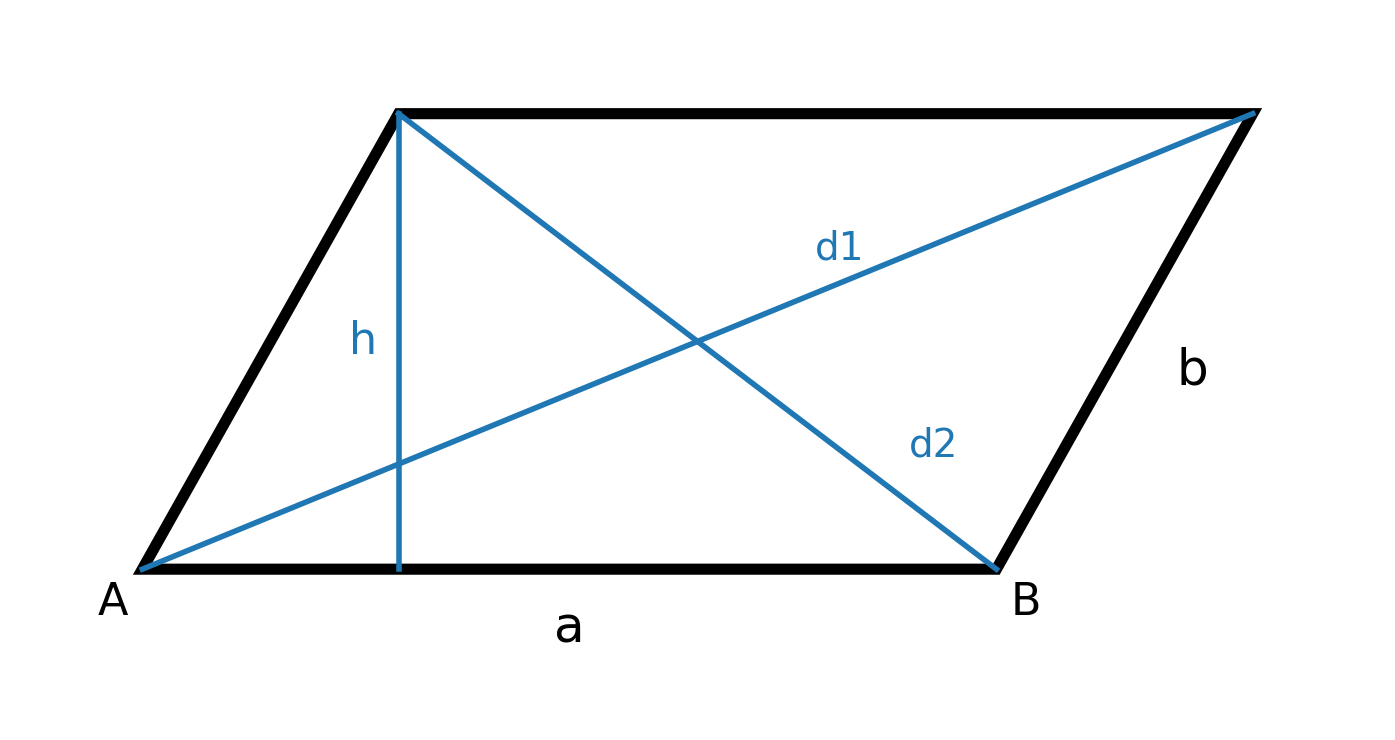
Parallelogramm

 

Es gibt keine rechten Winkel in einem Parallelogramm, aber die gegenüberliegenden Winkel sind immer gleich. Die Summe zweier benachbarter Winkel beträgt 180°.

 

$$ \large \angle A + \angle B = 180^\circ $$

 

Eine besondere Variante des Parallelogramms wird Raute genannt. Hier sind alle vier Seiten gleich lang. Genauso wie ein gleichseitiges Rechteck ein Quadrat genannt wird.

 

Der Schnittpunkt der Diagonalen in einem Parallelogramm ist gleichzeitig ihr Mittelpunkt.

Das bedeutet, dass die Diagonalen sich gegenseitig in zwei gleich große Teile teilen, aber sie stehen nicht notwendigerweise senkrecht aufeinander.

 

Eigenschaften eines Parallelogramms

  • Gegenüberliegende Seiten sind gleich lang.
  • Gegenüberliegende Seiten sind parallel.
  • Gegenüberliegende Winkel sind gleich groß.
  • Benachbarte Winkel ergeben zusammen 180°.
  • Der Schnittpunkt der Diagonalen ist auch ihr Mittelpunkt.
  • Ein Parallelogramm kann entlang einer Diagonalen in zwei kongruente Dreiecke geteilt werden.

 

Bei Berechnungen mit einem Parallelogramm ist es oft notwendig, Trigonometrie und Dreiecksberechnungen zu verwenden.

 

 

Rechner

Formeln

Seite a

$$ a=\frac{Area}{h} $$

$$ a=\frac{Area}{b\cdot sin(A)} $$

$$ a=\frac{P-(2\cdot b)}{2} $$

$$ a = \begin{cases} \sqrt{d_1^2 - h^2} + \sqrt{b^2 - h^2}, & A < 90^\circ \\[6pt] \sqrt{d_1^2 - h^2} - \sqrt{b^2 - h^2}, & A > 90^\circ \end{cases} $$

$$ a = \begin{cases} \sqrt{d_2^2 - h^2} - \sqrt{b^2 - h^2}, & A > 90^\circ \\[6pt] \sqrt{d_2^2 - h^2} + \sqrt{b^2 - h^2}, & A < 90^\circ \end{cases} $$

Seite b

$$ b=\frac{h}{sin(A)} $$

$$ b=\frac{Area}{a\cdot sin(A)} $$

$$ b=\frac{P-(2\cdot a)}{2} $$

$$ b = \sqrt{\Bigl(\sqrt{d_1^2 - h^2} - a\Bigr)^2 + h^2} $$

$$ b = \sqrt{\Bigl(a - \sqrt{d_2^2 - h^2}\Bigr)^2 + h^2} $$

Höhe

$$ h = b \cdot \sin(A) $$

$$ h = \frac{\text{Area}}{a} $$

Diagonale 1

$$ d_1 = \sqrt{a^2 + b^2 - 2ab \cos(A)} $$

Diagonale 2

$$ d_2 = \sqrt{a^2 + b^2 + 2ab \cos(A)} $$

Winkel A

$$ \angle A=180-B $$

$$ \angle A=sin^{-1}\biggl(\frac{h}{b}\biggr) $$

$$ \angle A = sin^{-1}\Bigl(\tfrac{\text{Area}}{a \cdot b}\Bigr) $$

$$ \angle A = cos^{-1}\Bigl(\tfrac{a^2 + b^2 - d_1^2}{2ab}\Bigr) $$

$$ \angle A = cos^{-1}\Bigl(\tfrac{d_2^2 - a^2 - b^2}{2ab}\Bigr) $$

Winkel B

$$ B = 180 - A $$

$$ B = \sin^{-1}\!\Bigl(\tfrac{h}{a}\Bigr) $$

$$ B = \sin^{-1}\!\Bigl(\tfrac{\text{Area}}{a \cdot b}\Bigr) $$

Fläche

$$ A = a \cdot h $$

$$ A= a \cdot b \cdot \sin(\angle A) $$

Umfang

$$ P = 2a + 2b $$

$$ P=2\cdot\biggl(\frac{h}{sin(A)}+\frac{Area}{h}\biggr) $$