Raute
Eine Raute ist ein schiefes Quadrat und ähnelt stark einem Parallelogramm, das ein schiefes Rechteck ist.
Man kann auch sagen, dass alle Quadrate Rauten sind, aber nicht alle Rauten Quadrate, weil die Winkel einer Raute nicht unbedingt 90 Grad betragen müssen.
Die Raute ist in der Praxis oft leicht zu berechnen, weil alle Seiten gleich lang sind wie bei einem Quadrat.
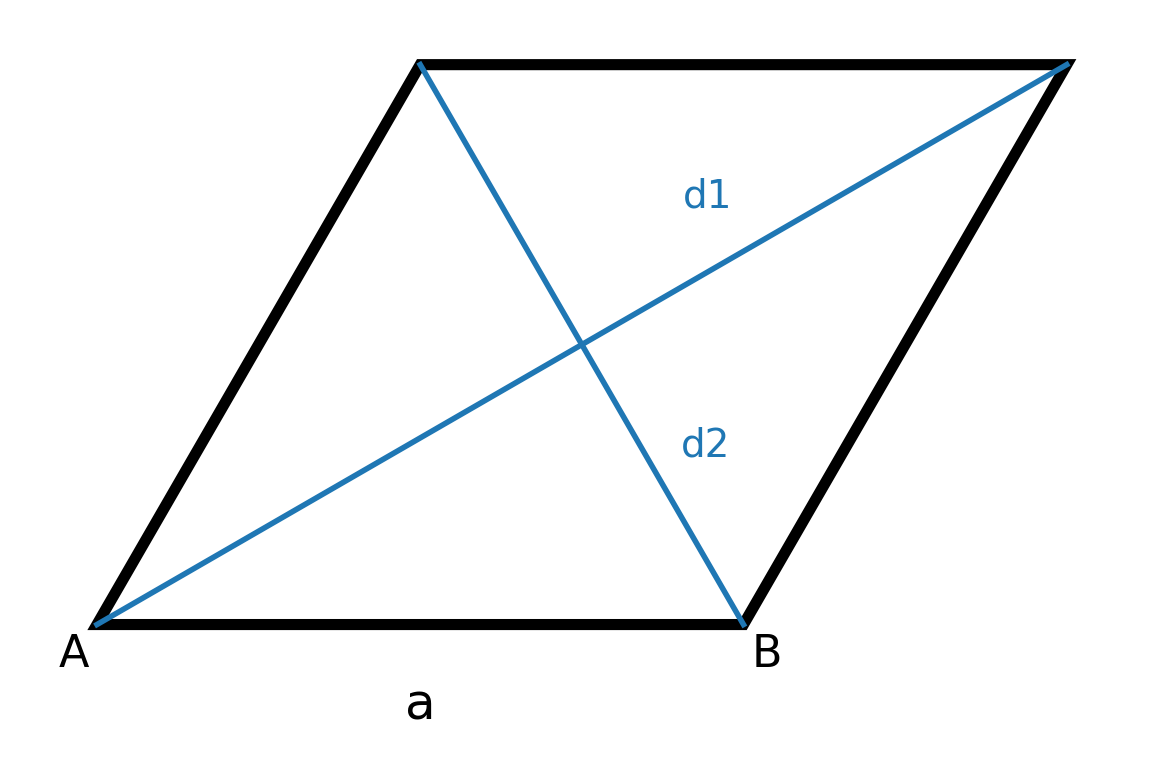
Eigenschaften, die eine Raute kennzeichnen
- Alle vier Seiten sind gleich lang.
- Gegenüberliegende Seiten sind parallel.
- Gegenüberliegende Winkel sind gleich groß, und benachbarte Winkel ergeben zusammen 180 Grad.
- Der Schnittpunkt der Diagonalen ist zugleich ihr Mittelpunkt.
- Die Diagonalen stehen senkrecht aufeinander.
- Jede Diagonale halbiert die angrenzenden Winkel, sodass die Figur zwei Symmetrieachsen entlang der Diagonalen hat.
- Die Raute kann in vier kongruente rechtwinklige Dreiecke unterteilt werden.
Dass die Diagonalen sich halbieren und senkrecht stehen, bedeutet, dass man die Raute in rechtwinklige Dreiecke zerlegen kann.
Damit kann man den Satz des Pythagoras und die elementare Trigonometrie für Berechnungen verwenden.