Ein wichtiger Teil der Mengenlehre ist das Vergleichen und Kombinieren von Mengen. Hier betrachten wir Teilmengen, echte Teilmengen, Schnittmengen, Potenzmengen und das kartesische Produkt.

 

Teilmengen

Eine Menge \( \large A\) ist eine Teilmenge einer anderen Menge \( \large B\), wenn alle Elemente von \( \large A\) auch in \( \large B\) enthalten sind. Man schreibt:

 

$$ \large A \subseteq B $$

 

 

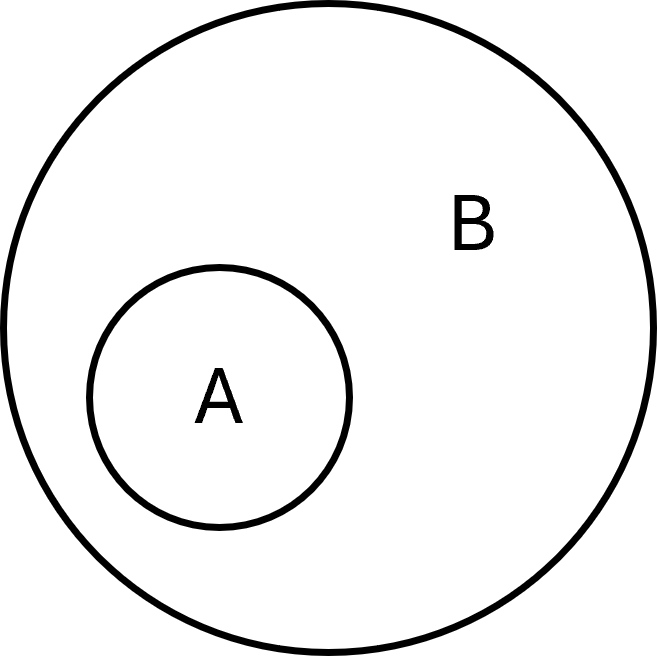
Formal kann man das so definieren:

 

$$ \large A \subseteq B \;\;\Leftrightarrow\;\; \forall x \in A \Rightarrow x \in B $$

 

Beispiele:

 

• \( \large \{1,2\} \subseteq \{1,2,3,4\}\)
• Die leere Menge ist immer eine Teilmenge: \( \large \emptyset \subseteq A\) für jede Menge \( \large A\).

 

Hinweis: In manchen Büchern wird das Symbol \( \large \subset\) anstelle von \( \large \subseteq\) für Teilmengen verwendet. Hier benutzen wir \( \large \subseteq\) als Standard.

 

 

Echte Teilmenge

Eine Menge \( \large A\) ist eine echte Teilmenge von \( \large B\), wenn \( \large A \subseteq B\), aber \( \large A \neq B\).

Das bedeutet, dass \( \large B\) mindestens ein Element enthält, das nicht in \( \large A\) liegt.

Die Notation lautet:

 

$$ \large A \subset B $$

 

Beispiel: \( \large \{1,2\} \subset \{1,2,3\}\).

 

 

Schnittmenge

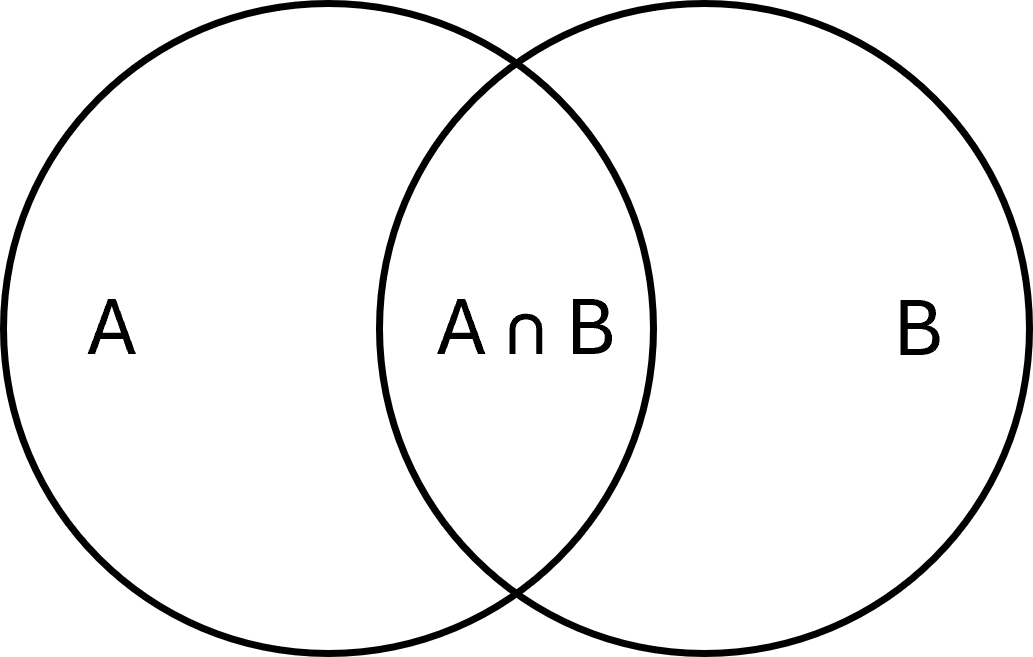
Die Schnittmenge zweier Mengen \( \large A\) und \( \large B\) ist die Menge der Elemente, die in beiden Mengen enthalten sind. Sie wird geschrieben als:

 

$$ \large A \cap B = \{x \mid x \in A \;\wedge\; x \in B\} $$

 

Beispiel: Wenn \( \large A = \{1,2,3\}\) und \( \large B = \{3,4,5\}\), dann gilt \( \large A \cap B = \{3\}\).

 

 

 

 

Potenzmenge

Die Potenzmenge einer Menge \( \large A\) ist die Menge aller Teilmengen von \( \large A\).

Sie wird geschrieben als \( \large \mathcal{P}(A)\).

 

Wenn \( \large A = \{0,1\}\), dann gilt:

 

$$ \large \mathcal{P}(A) = \{\emptyset, \{0\}, \{1\}, \{0,1\}\} $$

 

Die Anzahl der Elemente einer Potenzmenge ist \( \large 2^{|A|}\).

Zum Beispiel: Wenn \( \large |A| = 3\), dann hat \( \large \mathcal{P}(A)\) \( \large 2^3 = 8\) Elemente.

 

 

Kartesisches Produkt

Das kartesische Produkt zweier Mengen \( \large A\) und \( \large B\) ist die Menge aller geordneten Paare, wobei die erste Komponente aus \( \large A\) und die zweite aus \( \large B\) stammt.

Es wird geschrieben als:

 

$$ \large A \times B = \{(a,b) \mid a \in A \;\wedge\; b \in B\} $$

 

Beispiel: Wenn \( \large A = \{1,2\}\) und \( \large B = \{a,b\}\), dann gilt:

 

$$ \large A \times B = \{(1,a),(1,b),(2,a),(2,b)\} $$

 

Beachte, dass die Reihenfolge eine Rolle spielt: \( \large A \times B \neq B \times A\) im Allgemeinen.