Mengenoperationen sind Methoden zum Kombinieren oder Vergleichen von Mengen. Hier betrachten wir die Vereinigung, den Schnitt, disjunkte Mengen, die Differenz, das Komplement und wie diese mit Venn-Diagrammen veranschaulicht werden können.

 

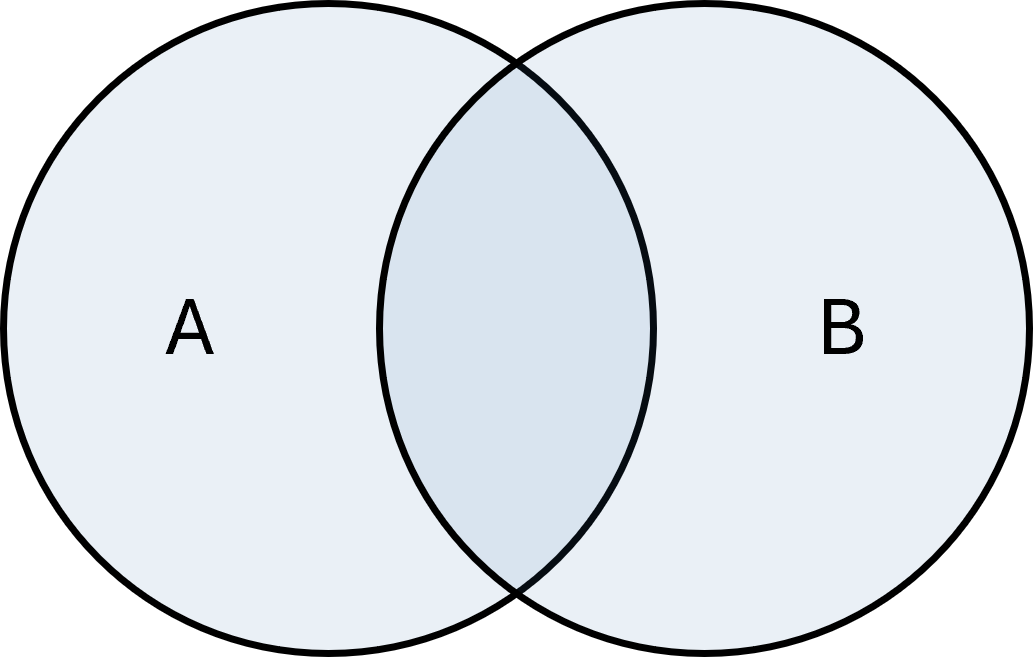
Vereinigung

Die Vereinigung zweier Mengen \( \large A\) und \( \large B\) ist die Menge aller Elemente, die in \( \large A\), in \( \large B\) oder in beiden enthalten sind. Sie wird geschrieben als:

 

$$ \large A \cup B = \{x \mid x \in A \;\vee\; x \in B\} $$

 

Beispiel: Wenn \( \large A = \{1,2,3\}\) und \( \large B = \{3,4,5\}\), dann ist \( \large A \cup B = \{1,2,3,4,5\}\).

 

 

 

 

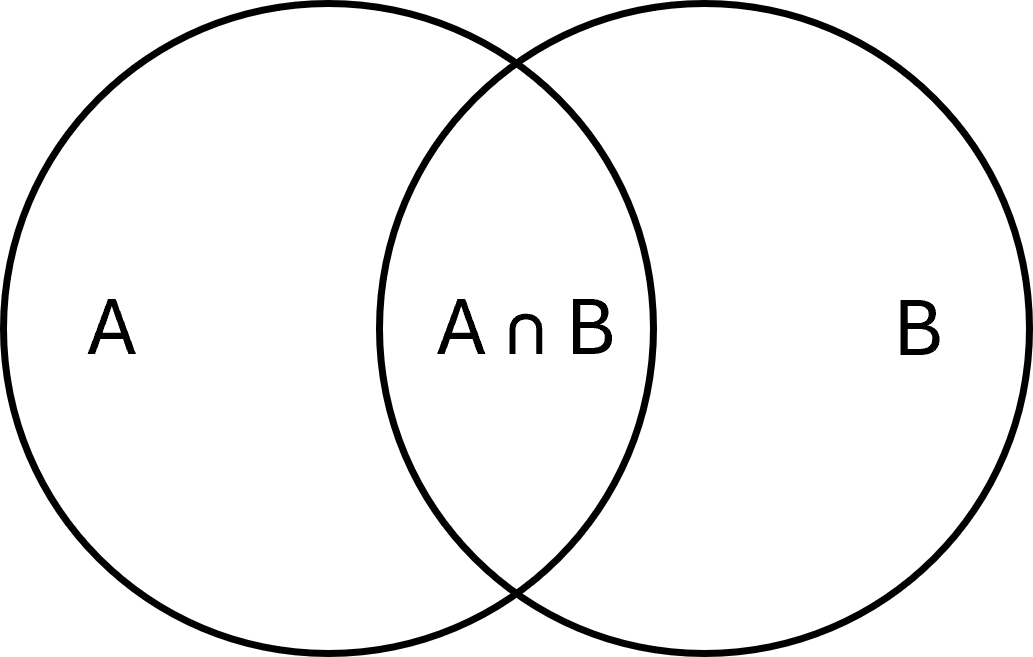
Schnittmenge

Die Schnittmenge zweier Mengen sind die Elemente, die sie gemeinsam haben. Sie wird geschrieben als:

 

$$ \large A \cap B = \{x \mid x \in A \;\wedge\; x \in B\} $$

 

Beispiel: Wenn \( \large A = \{1,2,3\}\) und \( \large B = \{3,4,5\}\), dann ist \( \large A \cap B = \{3\}\).

 

 

 

 

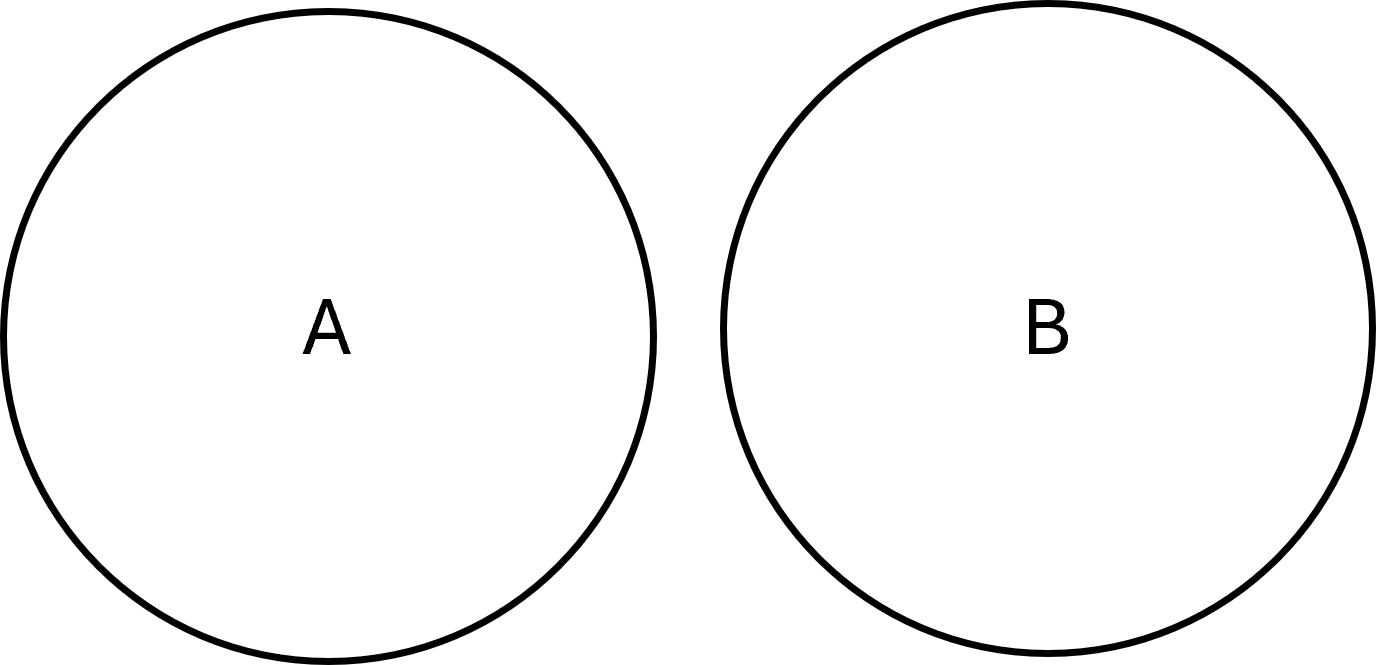
Disjunkte Mengen

Zwei Mengen sind disjunkt, wenn sie keine gemeinsamen Elemente haben. Das heißt, ihre Schnittmenge ist leer:

 

$$ \large A \cap B = \emptyset $$

 

Beispiel: \( \large A = \{1,2,3\}, B = \{4,5,6\}\).

 

 

 

 

Differenz

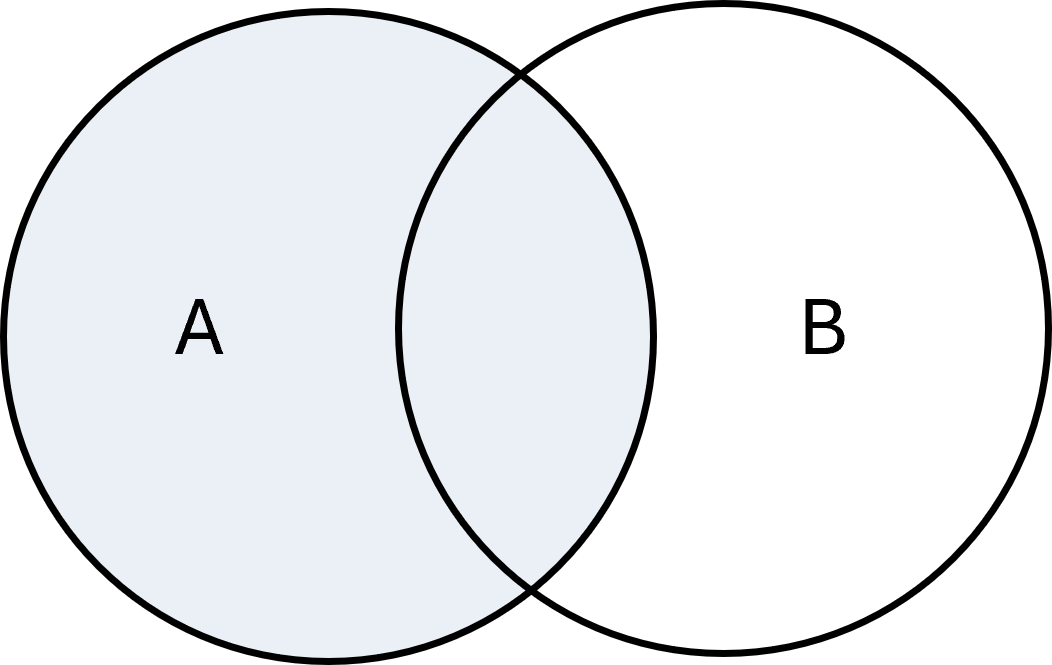
Die Differenz zweier Mengen \( \large A\) und \( \large B\), geschrieben als \( \large A - B\) oder \( \large A \setminus B\), sind die Elemente, die in \( \large A\), aber nicht in \( \large B\) enthalten sind:

 

$$ \large A - B = \{x \mid x \in A \;\wedge\; x \notin B\} $$

 

Beispiel: Wenn \( \large A = \{1,2,3\}, B = \{3,4,5\}\), dann ist \( \large A - B = \{1,2\}\).

 

 

 

 

Komplement

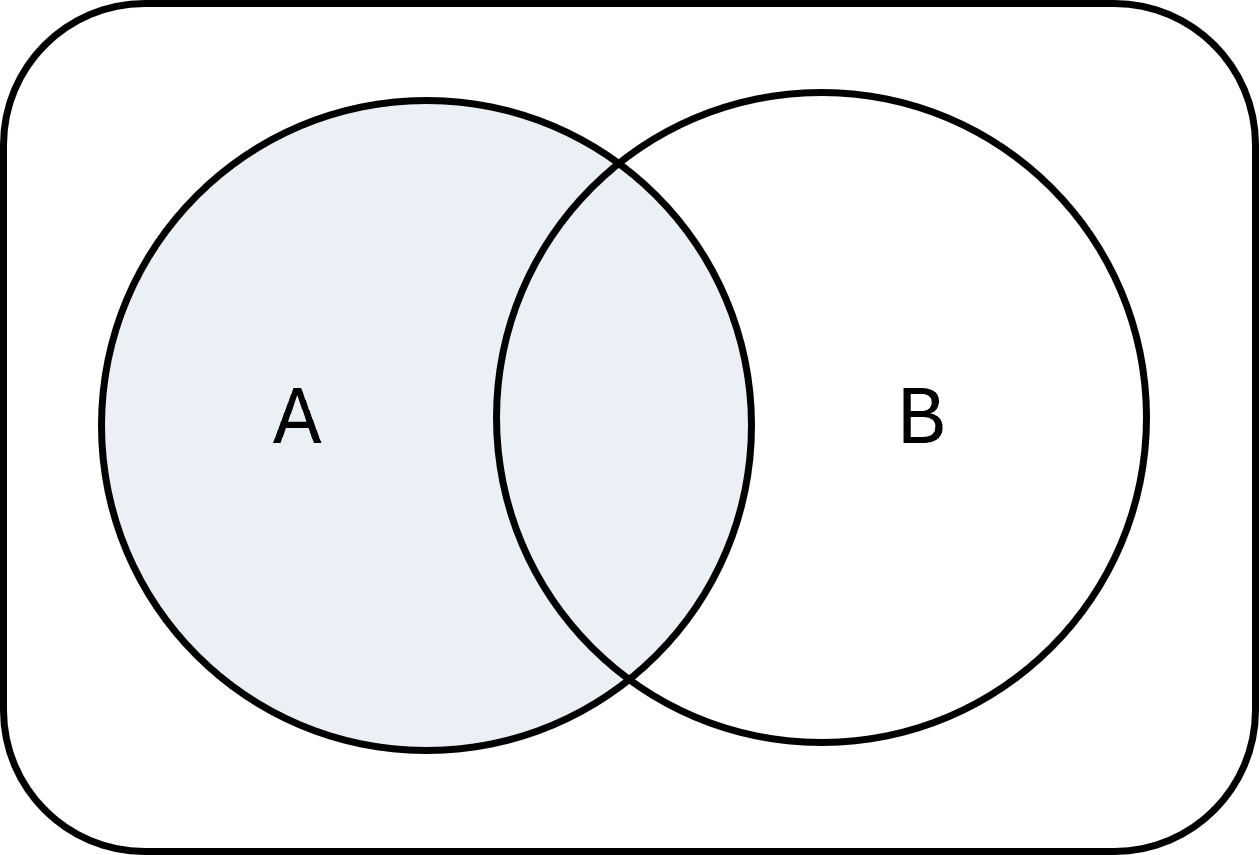
Wenn wir ein Universum \( \large U\) haben, das alle möglichen Elemente enthält, können wir das Komplement einer Menge \( \large A\) als alle Elemente in \( \large U\) definieren, die nicht in \( \large A\) enthalten sind. Es wird geschrieben als:

 

$$ \large A^{c} = \{x \in U \mid x \notin A\} $$

 

Beispiel: Wenn \( \large U = \{1,2,3,4,5\}\) und \( \large A = \{1,2\}\), dann ist \( \large A^{c} = \{3,4,5\}\).

 

 

 

 

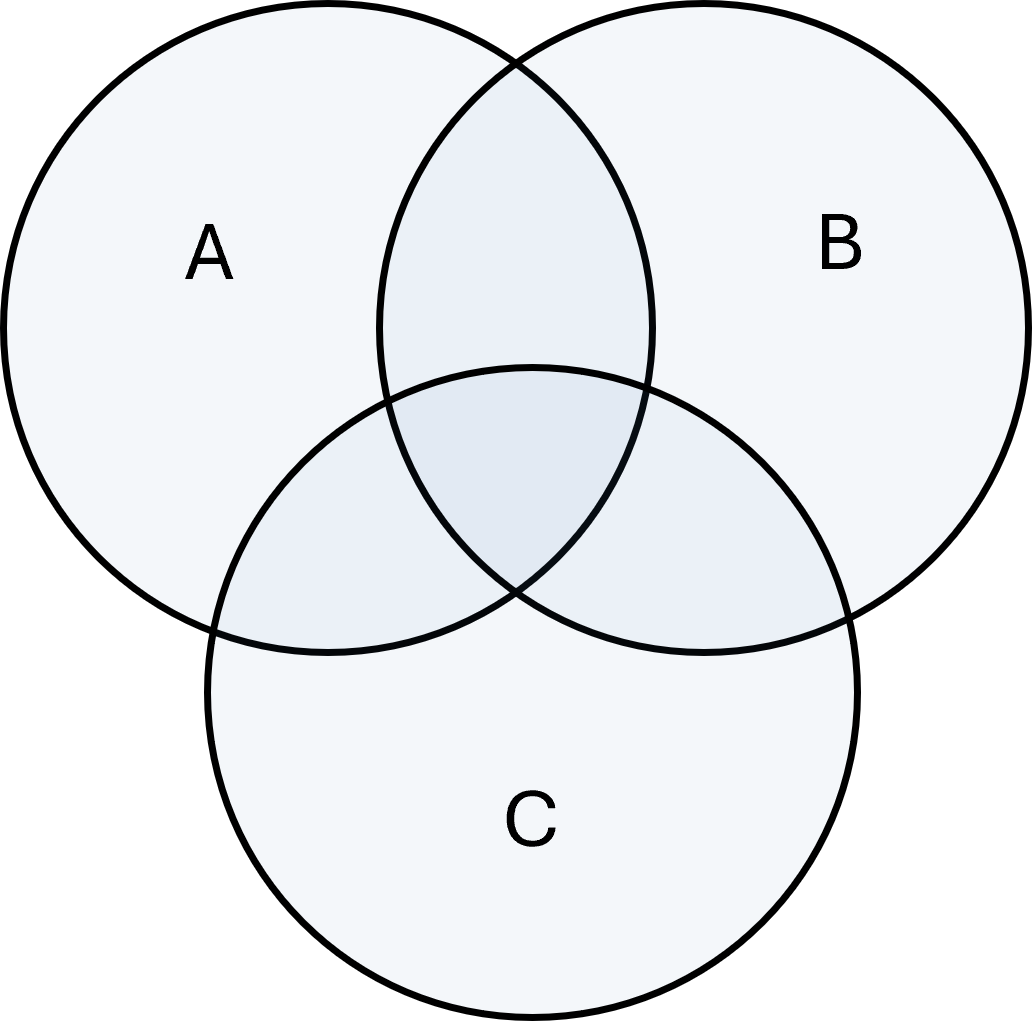
Venn-Diagramme

Venn-Diagramme werden oft verwendet, um Mengenoperationen grafisch darzustellen.

Kreise stellen Mengen dar, und überlappende Bereiche zeigen, wie Vereinigung, Schnittmenge, Differenz und Komplement funktionieren.