Inverse Funktionen

Eine Funktion ist bijektiv, wenn sie sowohl injektiv als auch surjektiv ist.

Das bedeutet, dass jedes Element der Definitionsmenge \( \large A\) genau einem Element der Zielmenge \( \large B\) entspricht und dass ganz \( \large B\) abgedeckt wird.

Damit existiert eine eindeutige Zuordnung, die umkehrbar ist.

 

 

Definition

Eine Funktion \( \large f : A \to B\) ist bijektiv, wenn:

 

$$ \large \forall a_1,a_2 \in A: f(a_1)=f(a_2) \Rightarrow a_1=a_2 \quad (\text{Injektivität}) $$

$$ \large \forall b \in B \;\exists a \in A : f(a)=b \quad (\text{Surjektivität}) $$

 

Die Kombination dieser beiden Eigenschaften stellt sicher, dass die Funktion „umkehrbar“ ist.

 

 

Existenz der Umkehrfunktion

Wenn \( \large f : A \to B\) bijektiv ist, existiert eine Umkehrfunktion \( \large f^{-1} : B \to A\), die erfüllt:

 

$$ \large f^{-1}(f(a)) = a \quad \text{für alle } a \in A $$

$$ \large f(f^{-1}(b)) = b \quad \text{für alle } b \in B $$

 

Die Umkehrfunktion „hebt“ die Wirkung der ursprünglichen Funktion auf.

 

 

Beispiele

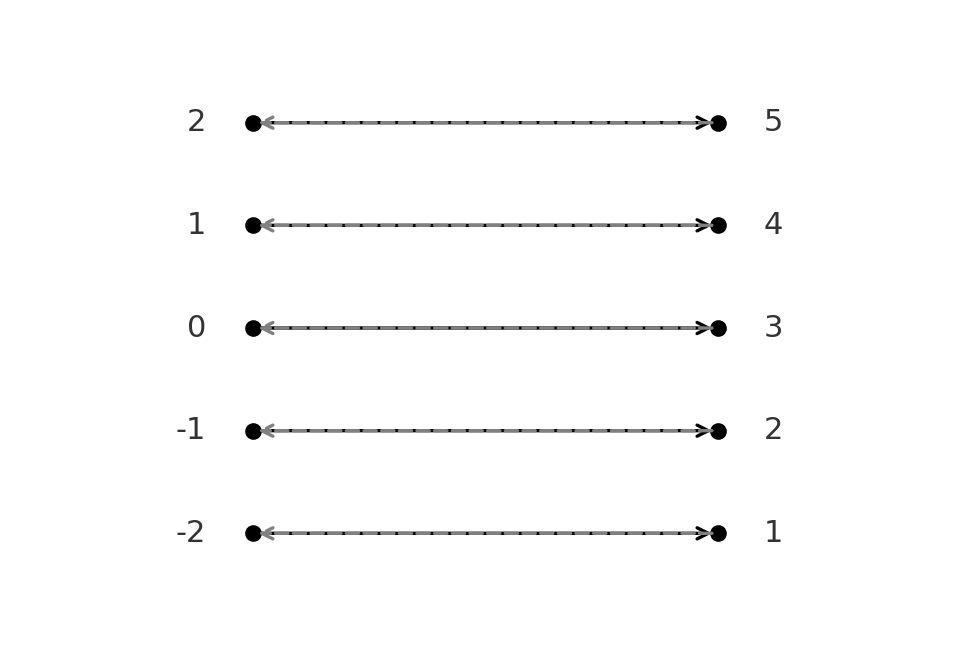
Bijektive Funktion: \( \large f(x)=x+3\) von \( \large \mathbb{Z} \to \mathbb{Z}\) ist bijektiv.

 

Die Umkehrfunktion ist \( \large f^{-1}(y)=y-3\).

 

 

Nicht-bijektive Funktion: \( \large f(x)=x^2\) von \( \large \mathbb{R} \to \mathbb{R}\) ist nicht bijektiv, weil sie nicht injektiv ist (sowohl \( \large -2\) als auch \( \large 2\) ergeben das Bild \( \large 4\)).

Daher existiert hier keine Umkehrfunktion.

 

 

Anwendung

Bijektive Funktionen und ihre Umkehrungen spielen eine zentrale Rolle in vielen Bereichen der Mathematik und Informatik:

 

• Kryptographie: Verschlüsselungsalgorithmen erfordern Funktionen, die eindeutig umkehrbar sind, damit Nachrichten wieder entschlüsselt werden können.
• Algebra: Isomorphismen zwischen algebraischen Strukturen sind Bijektionen, die die Struktur erhalten.
• Logik und Theorie: In mathematischen Beweisen werden Bijektionen verwendet, um die Größe von Mengen (Kardinalität) zu vergleichen.

 

Das Verständnis von bijektiven Funktionen ist daher entscheidend für theoretische und praktische Anwendungen.