Injektive, surjektive und bijektive Funktionen

In der Mathematik können Funktionen unterschiedliche Eigenschaften haben, je nachdem, wie die Elemente der Definitionsmenge und der Zielmenge verbunden sind.

Die drei wichtigsten sind injektiv, surjektiv und bijektiv.

Injektive Funktion

Eine Funktion $ \large f : A \to B$ ist injektiv, wenn zwei verschiedene Elemente in $ \large A$ immer unterschiedliche Bilder in $ \large B$ haben.

Mit anderen Worten:

$$ \large f(a_1) = f(a_2) \;\Rightarrow\; a_1 = a_2 $$

Beispiel:

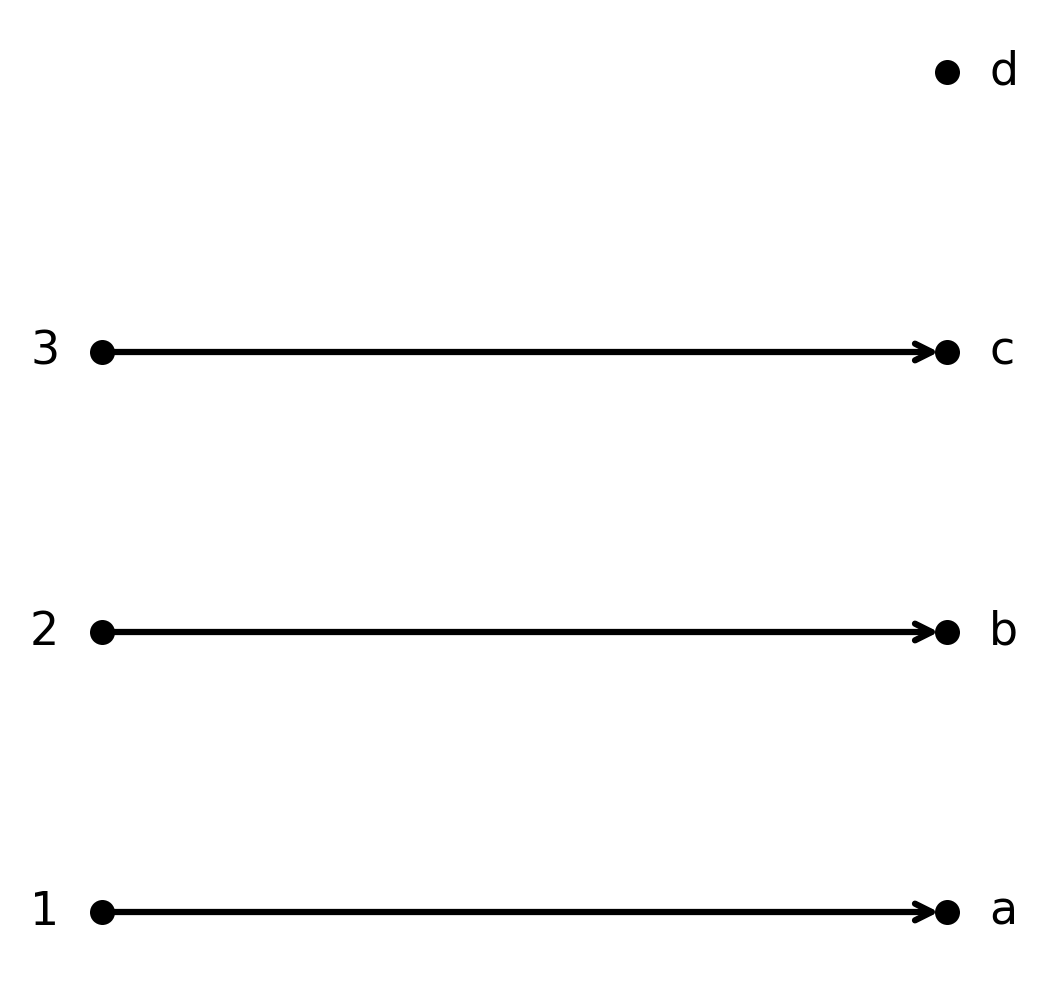
Die Funktion $ \large f : \{1,2,3\} \to \{a,b,c,d\}$ mit $ \large f(1)=a, f(2)=b, f(3)=c$ ist injektiv.

Jedes Element aus $ \large A$ wird einem eindeutigen Element in $ \large B$ zugeordnet, aber nicht die gesamte Zielmenge wird abgedeckt.

Injektive Funktion

Surjektive Funktion

Eine Funktion $ \large f : A \to B$ ist surjektiv, wenn jedes Element in $ \large B$ von mindestens einem Element aus $ \large A$ getroffen wird.

Das heißt:

$$ \large \forall b \in B, \;\exists a \in A : f(a) = b $$

Beispiel:

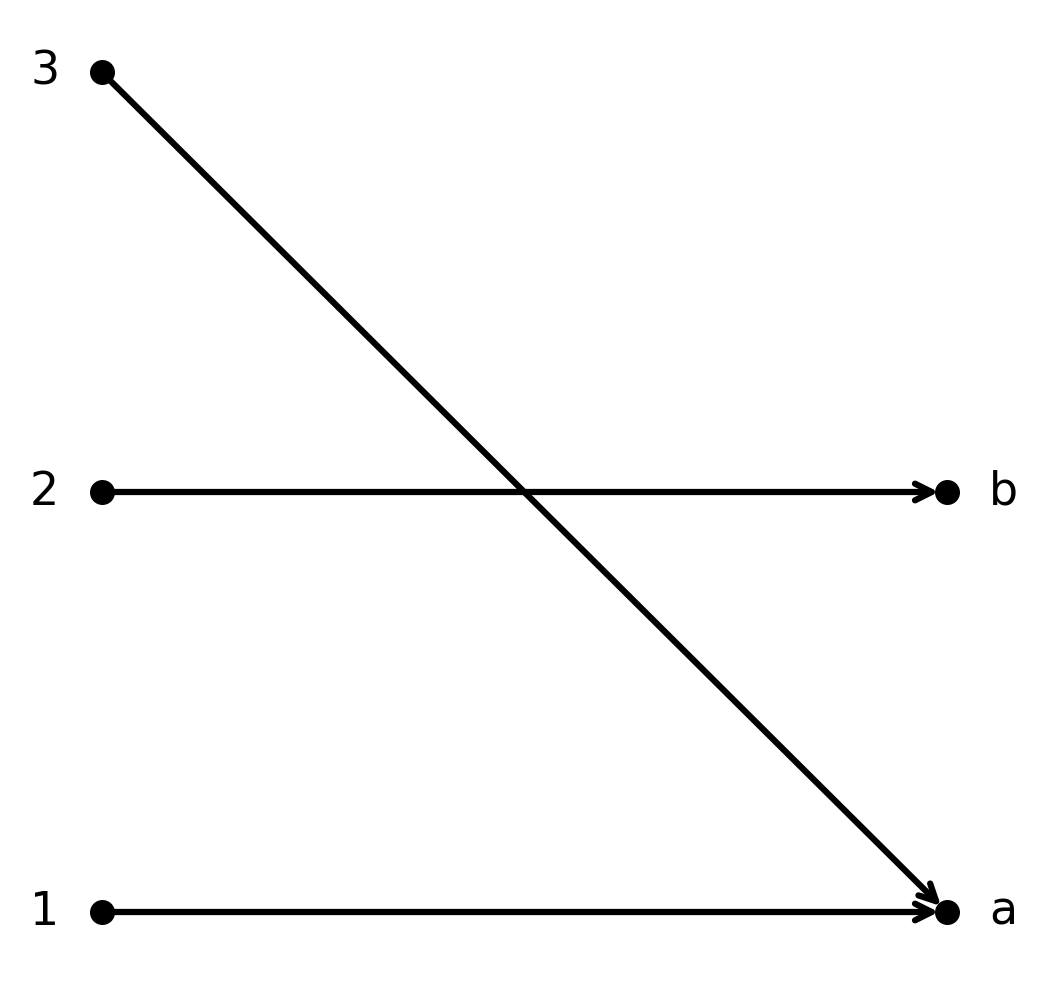
Die Funktion $ \large f : \{1,2,3\} \to \{a,b\}$ mit $ \large f(1)=a, f(2)=b, f(3)=a$ ist surjektiv.

Beide Elemente von $ \large B$ werden getroffen, aber die Funktion ist nicht injektiv, da $ \large 1$ und $ \large 3$ beide auf $ \large a$ abgebildet werden.

Surjektive Funktion

Bijektive Funktion

Eine Funktion ist bijektiv, wenn sie sowohl injektiv als auch surjektiv ist.

Das bedeutet, dass es eine eineindeutige Zuordnung zwischen den Elementen von $ \large A$ und $ \large B$ gibt. Jedes Element aus $ \large A$ wird einem eindeutigen Element in $ \large B$ zugeordnet, und die gesamte Zielmenge $ \large B$ wird abgedeckt.

Beispiel:

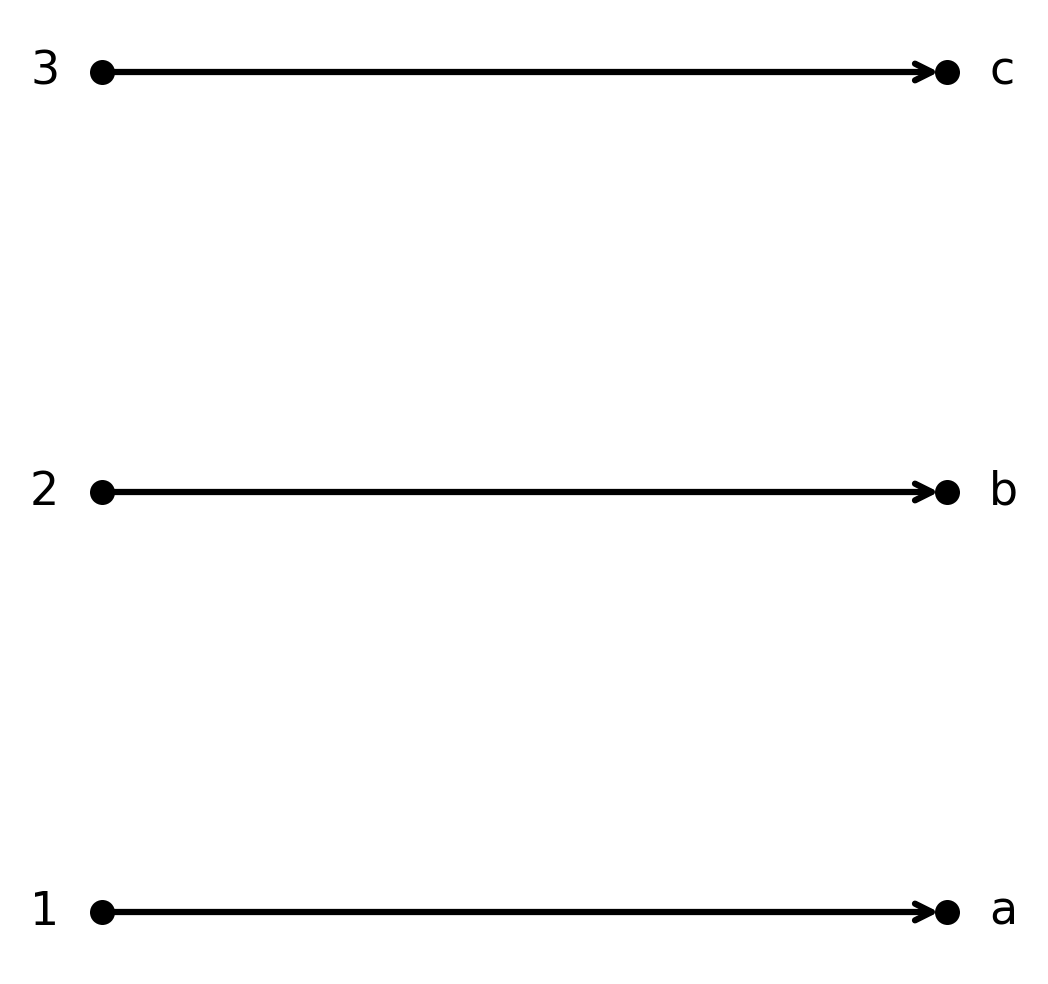
Die Funktion $ \large f : \{1,2,3\} \to \{a,b,c\}$ mit $ \large f(1)=a, f(2)=b, f(3)=c$ ist bijektiv.

Jedes Element aus $ \large A$ wird einem eindeutigen Element in $ \large B$ zugeordnet, und alle Elemente von $ \large B$ werden getroffen.

Bijektive Funktion

Zusammenfassung

Injektiv: Zwei verschiedene Eingaben ergeben immer unterschiedliche Ausgaben.
Surjektiv: Die gesamte Zielmenge wird abgedeckt.
Bijektiv: Kombination beider – es gibt eine eineindeutige Zuordnung, die umkehrbar ist.

Bijektive Funktionen sind besonders wichtig, da sie immer eine inverse Funktion besitzen, was es ermöglicht, vom Output zum Input zurückzugehen.