Beispiele für Funktionen

Um die Eigenschaften von Funktionen besser zu verstehen, betrachten wir hier konkrete Beispiele in den klassischen Zahlenmengen: die natürlichen Zahlen \( \large \mathbb{N}\), die ganzen Zahlen \( \large \mathbb{Z}\) und die reellen Zahlen \( \large \mathbb{R}\).

 

Beispiel 1: Injektive Funktion in \( \large \mathbb{N}\)

Die Funktion \( \large f : \mathbb{N} \to \mathbb{N}\) gegeben durch \( \large f(n) = 2n\).

 

$$ \large f(n) = 2n $$

 

 

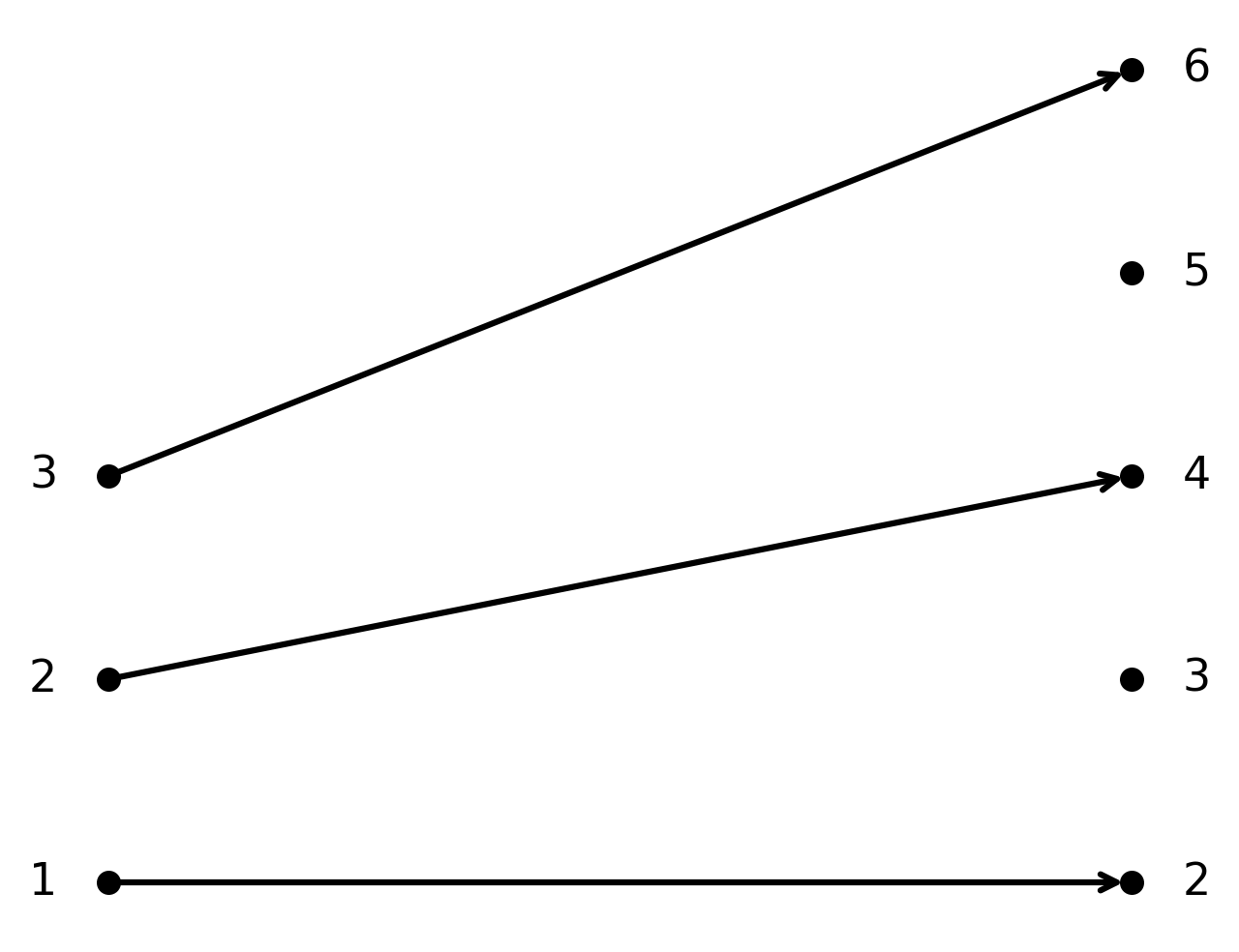
Injektive Funktion

 

Hier ist \( f\) injektiv, da zwei verschiedene natürliche Zahlen immer unterschiedliche Ergebnisse liefern, wenn sie mit 2 multipliziert werden. Aber die Funktion ist nicht surjektiv, da ungerade Zahlen nicht getroffen werden.

 

 

Beispiel 2: Surjektive Funktion in \( \large \mathbb{Z}\)

Die Funktion \( \large f : \mathbb{Z} \to \mathbb{Z}\) gegeben durch \( \large f(n) = \lfloor \frac{n}{2} \rfloor\).

 

$$ \large f(n) = \left\lfloor \frac{n}{2} \right\rfloor $$

 

 

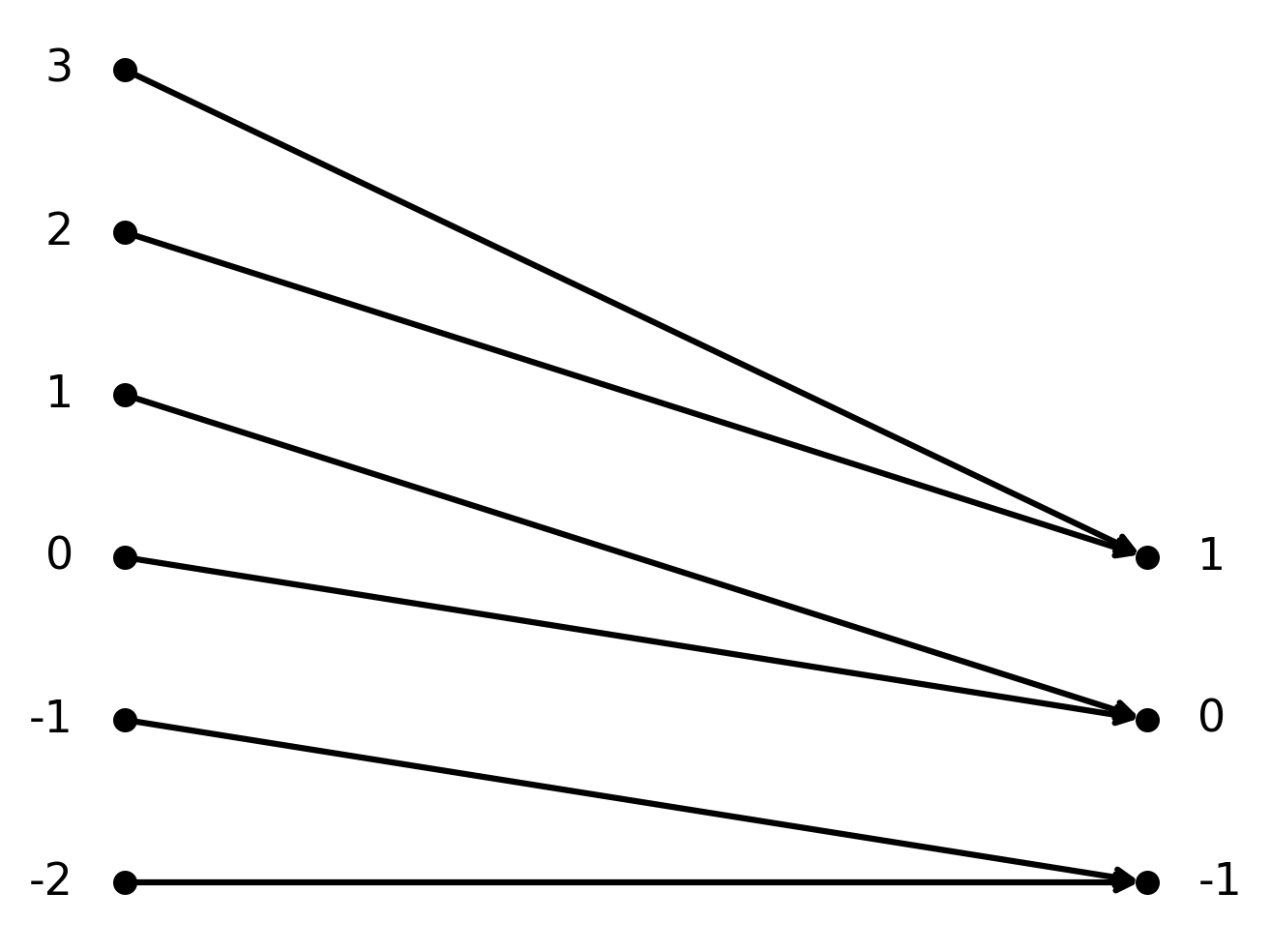
Surjektive Funktion

 

Hier ist die Funktion surjektiv, da jede ganze Zahl von mindestens einem \( \large n\) getroffen wird. Zum Beispiel \(\large f(2)=1\) und \(\large f(3)=1\).

Andererseits ist die Funktion nicht injektiv, da mehrere Eingaben dasselbe Ergebnis liefern können.

 

 

Beispiel 3: Bijektive Funktion in \( \large \mathbb{Z}\)

Die Funktion \( \large f : \mathbb{Z} \to \mathbb{Z}\) gegeben durch \( \large f(n) = n+1\).

 

$$ \large f(n) = n+1 $$

 

Bijektive Funktion

 

Hier ist \(\large f\) bijektiv: jede ganze Zahl hat ein eindeutiges Ergebnis, und alle ganzen Zahlen werden getroffen.

Daher kann die Funktion mit einer Inversen umgekehrt werden: \(\large f^{-1}(n) = n-1\).

 

 

Beispiel 4: Funktionen in \( \large \mathbb{R}\)

In den reellen Zahlen finden wir viele Funktionen, die die Eigenschaften veranschaulichen:

 

  • \( \large f(x) = x^3 \) von \( \large \mathbb{R} \to \mathbb{R}\) ist bijektiv. Jede reelle Zahl hat ein eindeutiges Bild, und ganz \( \large \mathbb{R}\) wird abgedeckt.
  • \( \large f(x) = x^2 \) von \( \large \mathbb{R} \to \mathbb{R}\) ist nicht injektiv (weil \( f(2)=f(-2)\)), aber sie ist surjektiv, wenn man nur \( \large [0,\infty[\) als Zielmenge betrachtet.
  • \( \large f(x) = e^x \) von \( \large \mathbb{R} \to (0,\infty)\) ist bijektiv, da alle positiven reellen Zahlen eindeutig getroffen werden.

 

 

Zusammenfassung

Die Beispiele zeigen, dass die Eigenschaften von Funktionen davon abhängen:

 

  • Welche Mengen wir als Definitions- und Zielmenge betrachten.
  • Wie die Funktion Eingaben und Ausgaben verknüpft.

 

Die klassischen Zahlenmengen \( \large \mathbb{N}, \mathbb{Z}, \mathbb{R}\) liefern viele gute und einfache Beispiele für injektive, surjektive und bijektive Funktionen.