Differentialligninger
En differentialligning beskriver sammenhængen mellem en funktion og dens afledte. I stedet for at fortælle direkte, hvad funktionen er, beskriver den, hvordan funktionen ændrer sig. Det gør differentialligninger til et centralt redskab i både matematik, fysik, biologi og økonomi, hvor mange fænomener netop handler om ændringer over tid.
Hvad er en differentialligning
En almindelig ligning indeholder en ukendt størrelse, fx \( \large x \). En differentialligning indeholder derimod en ukendt funktion \( \large y(x) \) og dens afledte, fx \( \large y'(x) \) eller \( \large y''(x) \). Målet er at finde den funktion \( \large y(x) \), som opfylder ligningen.
Eksempler:
$$ \large y' = 3x^2 $$
$$ \large y'' + y = 0 $$
Den første ligning siger, at hældningen på \( \large y \) altid er \( \large 3x^2 \). Den anden beskriver en svingning, fordi den kobler funktionen sammen med dens egen anden afledte.
Grundidéen
En differentialligning fortæller ikke direkte, hvordan grafen for \( \large y \) ser ud, men hvordan dens hældning ændrer sig fra punkt til punkt. Man kan derfor tænke på den som en opskrift på bevægelse eller vækst.
Hvis man kender den afledte, kan man finde funktionen ved at “gøre det omvendte” af differentiering – altså integrere. Derfor hænger differentialligninger tæt sammen med integralregning.
Ordnede og typer
En ordinær differentialligning (forkortet ODE) indeholder kun én uafhængig variabel, typisk \( \large x \) eller \( \large t \). Hvis ligningen indeholder flere variable og afledte med hensyn til flere variable, kaldes den en partiel differentialligning (PDE).
Ordnen af en differentialligning er den højeste afledte, der indgår. Fx:
- \( \large y' = 3x^2 \) → 1. ordens ligning
- \( \large y'' + y = 0 \) → 2. ordens ligning
Løsning af simple differentialligninger
De enkleste differentialligninger kan løses direkte ved integration. Hvis man fx har
$$ \large y' = 3x^2 $$
kan man finde \( \large y(x) \) ved at integrere højresiden:
$$ \large y = \int 3x^2 \, dx = x^3 + C $$
Her er \( \large C \) integrationskonstanten, som repræsenterer alle mulige løsninger – altså alle grafer med samme hældningsmønster, men forskellig placering.
Separation af variable
En almindelig metode til at løse 1. ordens ligninger er separation af variable. Hvis ligningen kan skrives som
$$ \large \frac{dy}{dx} = g(x) \cdot h(y) $$
kan man adskille \( \large x \) og \( \large y \) og integrere på hver side:
$$ \large \int \frac{1}{h(y)} \, dy = \int g(x) \, dx $$
Eksempel: Løs \( \large y' = 2xy \).
Adskil variable: \( \large \frac{1}{y} dy = 2x dx \).
Integrér begge sider:
$$ \large \ln|y| = x^2 + C $$
Omskriv til den generelle løsning:
$$ \large y = A e^{x^2} $$
hvor \( \large A = e^C \) er en konstant. Denne metode virker hver gang, variablene kan adskilles på denne måde.
Lineære differentialligninger af 1. orden
En lineær 1. ordens ligning har formen:
$$ \large y' + p(x)y = q(x) $$
Løsningen findes ved at gange hele ligningen med en integrerende faktor:
$$ \large \mu(x) = e^{\int p(x)\,dx} $$
Hermed kan ligningen skrives som
$$ \large (\mu(x)y)' = \mu(x)q(x) $$
og derefter integreres direkte. Denne metode kaldes integrerende faktor-metoden.
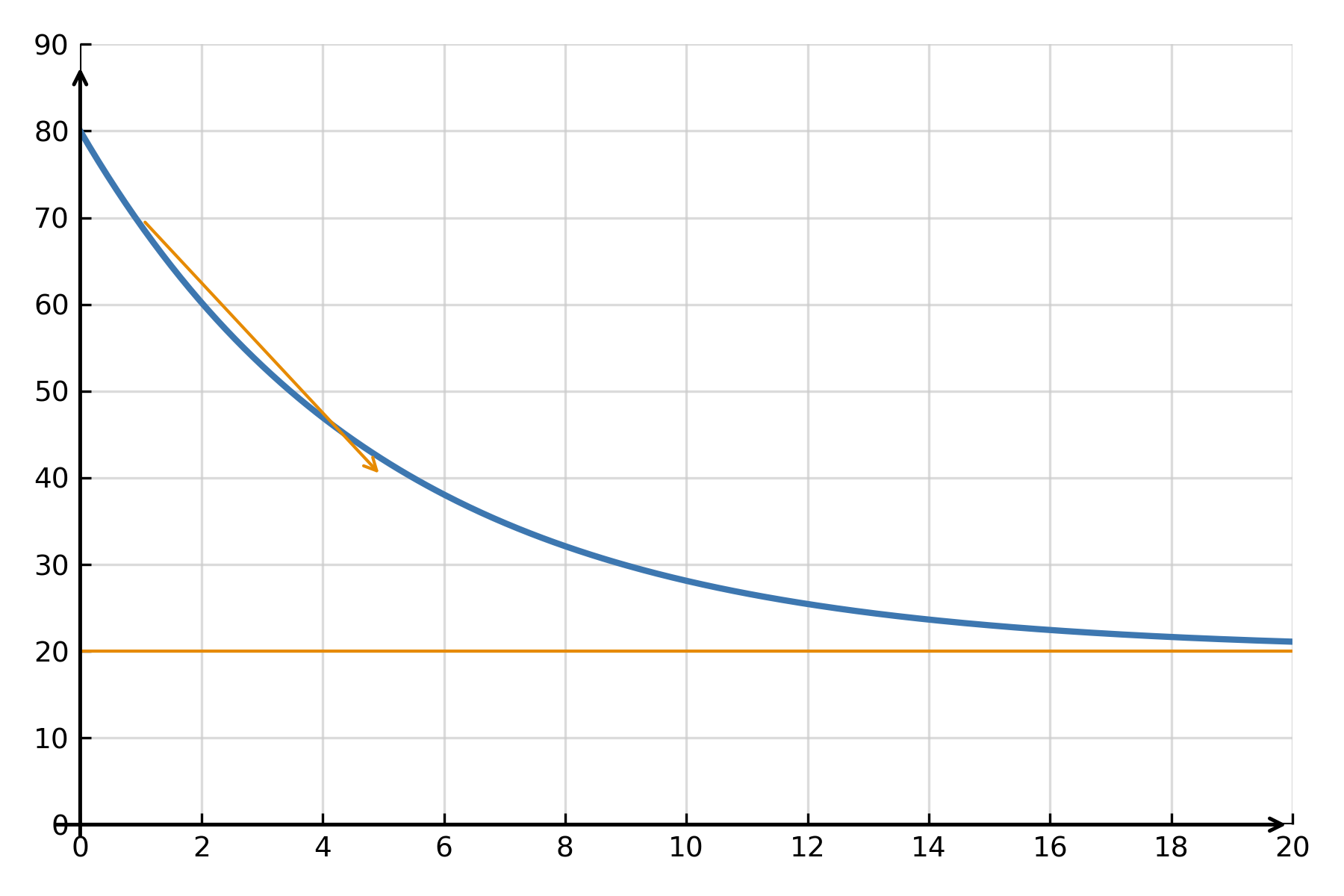
Eksempel: Kølingsloven
Et klassisk eksempel på en lineær differentialligning er Newtons kølingslov:
$$ \large \frac{dT}{dt} = -k(T - T_{\text{omg}}) $$
Her beskriver \( \large T(t) \) temperaturen af et objekt, der afkøles mod omgivelserne med temperaturen \( \large T_{\text{omg}} \), og \( \large k \) er en konstant. Løsningen viser, at temperaturen nærmer sig omgivelsernes eksponentielt:
$$ \large T(t) = T_{\text{omg}} + (T_0 - T_{\text{omg}})e^{-kt} $$
Sådan en ligning optræder også i forbindelse med radioaktivt henfald, afladning af kondensatorer og økonomiske modeller for tilpasning.
Andenordens differentialligninger
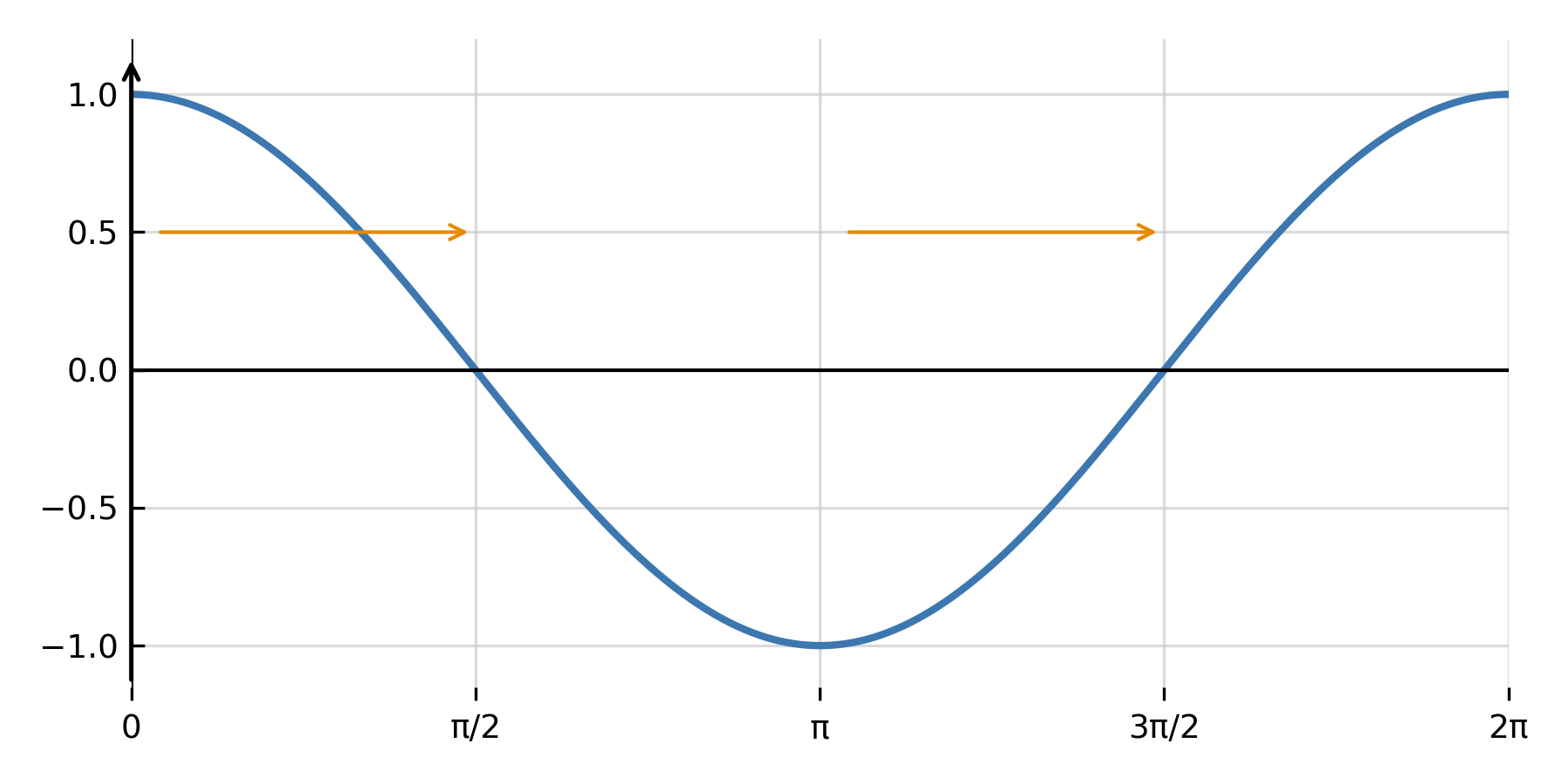
Når den anden afledte indgår, beskriver ligningen ofte bevægelse eller svingninger. Et vigtigt eksempel er harmoniske svingninger:
$$ \large y'' + \omega^2 y = 0 $$
Løsningen er en kombination af sinus og cosinus:
$$ \large y = A \cos(\omega x) + B \sin(\omega x) $$
Her beskriver \( \large A \) og \( \large B \) begyndelsesbetingelserne, mens \( \large \omega \) angiver svingningshastigheden. Denne type ligning bruges i alt fra mekanik og bølger til elektriske kredsløb.
Numeriske løsninger
I mange tilfælde kan en differentialligning ikke løses analytisk. I stedet bruger man numeriske metoder, hvor man beregner funktionen punkt for punkt ud fra dens afledte. De mest kendte metoder er Eulers metode, Runge–Kutta og Sekantmetoden, som alle gennemgås i afsnittet Numeriske metoder.
Opsummering
Differentialligninger beskriver, hvordan funktioner ændrer sig, og spiller en central rolle i al anvendt matematik. De bruges til at modellere vækst, bevægelse, svingninger, varme, strøm og mange andre fænomener. Nogle kan løses ved håndkraft, andre kræver numeriske metoder, men fælles for dem alle er, at de knytter differentialregning og integralregning sammen i et samlet system.