Variance et écart type
Dispersion
La dispersion indique dans quelle mesure les observations varient autour de la moyenne.
Si toutes les observations sont proches de la moyenne, la dispersion est faible. Si elles sont éloignées de la moyenne, la dispersion est grande.
Variance
La variance mesure la distance quadratique moyenne par rapport à la moyenne.
Pour trouver la variance, il faut :
- Soustraire la moyenne à chaque observation
- Élever les différences au carré
- Calculer la moyenne des différences au carré
$$ s^2 = \frac{(x_1 - \overline{x})^2 + (x_2 - \overline{x})^2 + ... + (x_n - \overline{x})^2}{n} $$
Écart-type
L’écart-type est la racine carrée de la variance. Il indique, dans la même unité que les observations, de combien elles s’écartent en moyenne de la moyenne.
$$ s = \sqrt{s^2} $$
Exemple
Nous utilisons l’observation des tailles des élèves.
- La moyenne est \( \overline{x} = 164{,}8 \)
- La variance est \( s^2 = 40{,}36 \)
- L’écart-type est \( s \approx 6{,}35 \)
Cela signifie que les tailles s’écartent en moyenne d’environ 6,35 cm de la moyenne.
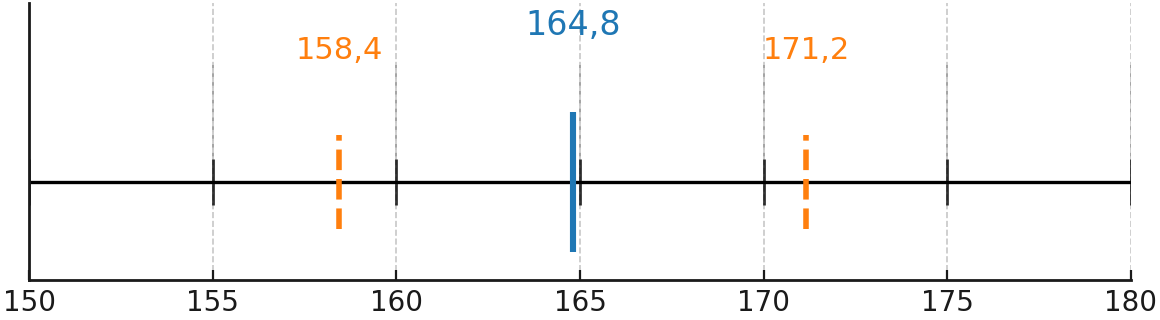
Diagramme
L’écart-type peut être représenté dans un diagramme, où la moyenne est marquée et les intervalles \( \overline{x} \pm s \) sont indiqués.