Fréquence relative
Que nous dit la fréquence
La fréquence exprime quel pourcentage représente une observation du nombre total d’observations.
Nous avons rassemblé nos observations ainsi :
- 150-159 cm de hauteur fréquence absolue = 2, fréquence relative = 20 %
- 160-169 cm de hauteur fréquence absolue = 5, fréquence relative = 50 %
- 170-179 cm de hauteur fréquence absolue = 3, fréquence relative = 30 %
Notre nombre total d’observations n = 10
On calcule ainsi :
$$ \text{150-159 cm} = \frac{2}{10} = 0,20 = 20\% $$
Formule
On peut l’écrire sous forme de formule comme ceci :
$$ Fréquence=\frac{fréquence\ absolue}{\text{nombre d’observations}} \Leftrightarrow $$
$$ f(x) = \frac{h(x)}{n} $$
Si tu additionnes toutes tes fréquences, elles doivent toujours donner 100 %
Ou 1, si tu calcules avec des décimales.
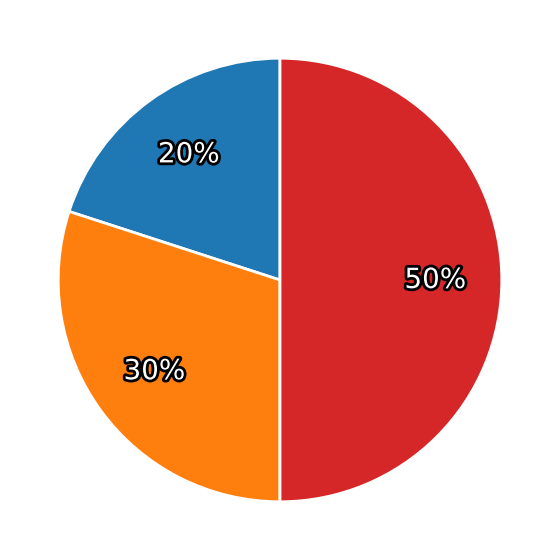
On peut aussi représenter les fréquences dans un diagramme.
Un diagramme circulaire (souvent appelé "camembert") est pratique pour montrer une répartition en pourcentage, mais si tu dois le dessiner à la main, un diagramme carré ou un diagramme empilé est plus simple.
Diagramme de fréquences
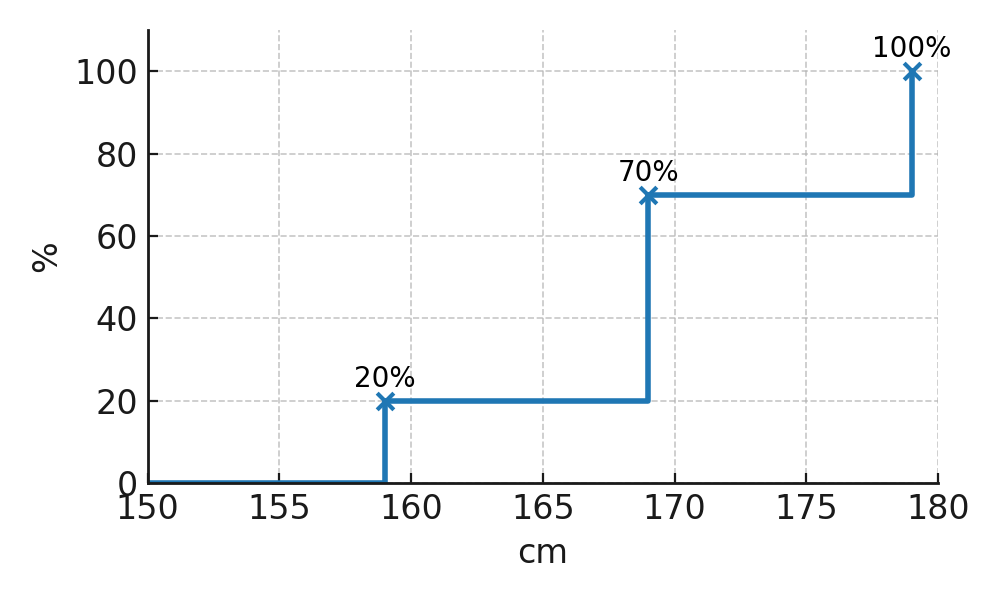
Fréquences cumulées
Une fréquence cumulée montre quel pourcentage des observations est inférieur ou égal à une limite donnée.
Autrement dit, on additionne les fréquences étape par étape.
| Intervalle | Fréquence | Fréquence cumulée |
|---|---|---|
| 150-159 cm | 20 % | 20 % |
| 160-169 cm | 50 % | 70 % |
| 170-179 cm | 30 % | 100 % |
D’après le tableau, on voit que 70 % des élèves mesurent au maximum 169 cm, et que tous (100 %) sont en dessous de 179 cm.
L’axe des x indique la taille en cm et l’axe des y la fréquence cumulée en pourcentage :