Fonctions inverses

Une fonction est bijective si elle est à la fois injective et surjective.

Cela signifie que chaque élément du domaine \( \large A\) correspond à exactement un élément du codomaine \( \large B\), et que tout \( \large B\) est couvert.

Ainsi, il existe une correspondance unique qui peut être inversée.

 

 

Définition

Une fonction \( \large f : A \to B\) est bijective si :

 

$$ \large \forall a_1,a_2 \in A: f(a_1)=f(a_2) \Rightarrow a_1=a_2 \quad (\text{injectivité}) $$

$$ \large \forall b \in B \;\exists a \in A : f(a)=b \quad (\text{surjectivité}) $$

 

La combinaison de ces deux propriétés garantit que la fonction peut être « inversée ».

 

 

Existence de la fonction inverse

Si \( \large f : A \to B\) est bijective, il existe une fonction inverse \( \large f^{-1} : B \to A\), qui satisfait :

 

$$ \large f^{-1}(f(a)) = a \quad \text{pour tout } a \in A $$

$$ \large f(f^{-1}(b)) = b \quad \text{pour tout } b \in B $$

 

L’inverse « annule » l’effet de la fonction originale.

 

 

Exemples

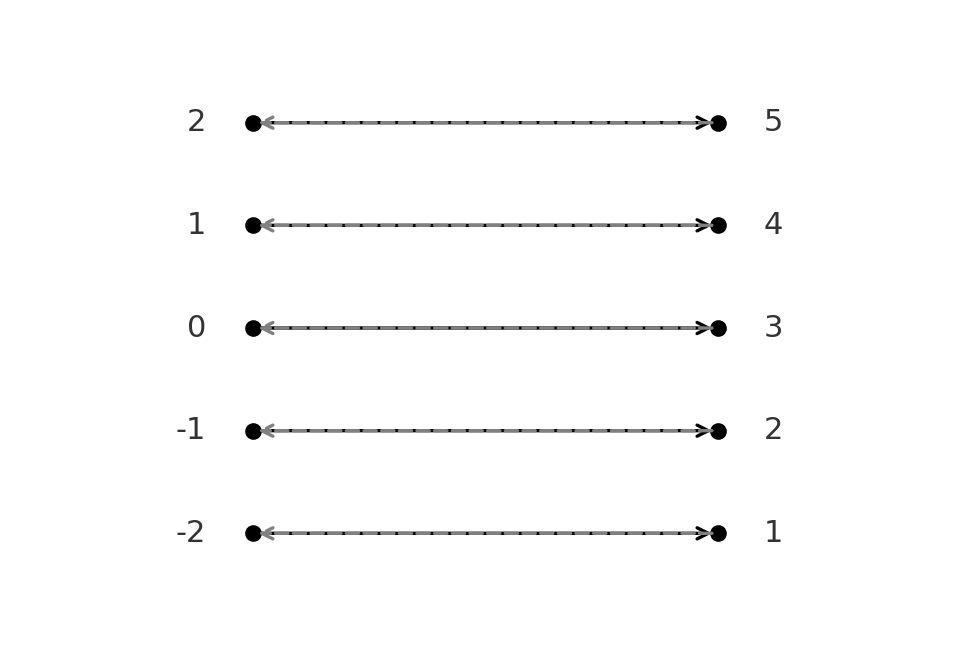
Fonction bijective : \( \large f(x)=x+3\) de \( \large \mathbb{Z} \to \mathbb{Z}\) est bijective.

 

La fonction inverse est \( \large f^{-1}(y)=y-3\).

 

 

Fonction non bijective : \( \large f(x)=x^2\) de \( \large \mathbb{R} \to \mathbb{R}\) n’est pas bijective, car elle n’est pas injective (à la fois \( \large -2\) et \( \large 2\) donnent l’image \( \large 4\)).

Par conséquent, il n’existe pas ici de fonction inverse.

 

 

Application

Les fonctions bijectives et leurs inverses jouent un rôle central dans de nombreux domaines des mathématiques et de l’informatique :

 

• Cryptographie : Les algorithmes de chiffrement nécessitent des fonctions qui peuvent être inversées de manière unique afin que les messages puissent être déchiffrés.
• Algèbre : Les isomorphismes entre structures algébriques sont des bijections qui préservent la structure.
• Logique et théorie : Dans les démonstrations mathématiques, les bijections sont utilisées pour comparer la taille des ensembles (cardinalité).

 

Comprendre les fonctions bijectives est donc essentiel pour les applications théoriques et pratiques.