Exemples de fonctions

Pour mieux comprendre les propriétés des fonctions, nous examinons ici des exemples concrets dans les ensembles numériques classiques : les nombres naturels \( \large \mathbb{N}\), les entiers \( \large \mathbb{Z}\) et les nombres réels \( \large \mathbb{R}\).

 

Exemple 1 : Fonction injective dans \( \large \mathbb{N}\)

La fonction \( \large f : \mathbb{N} \to \mathbb{N}\) définie par \( \large f(n) = 2n\).

 

$$ \large f(n) = 2n $$

 

 

 

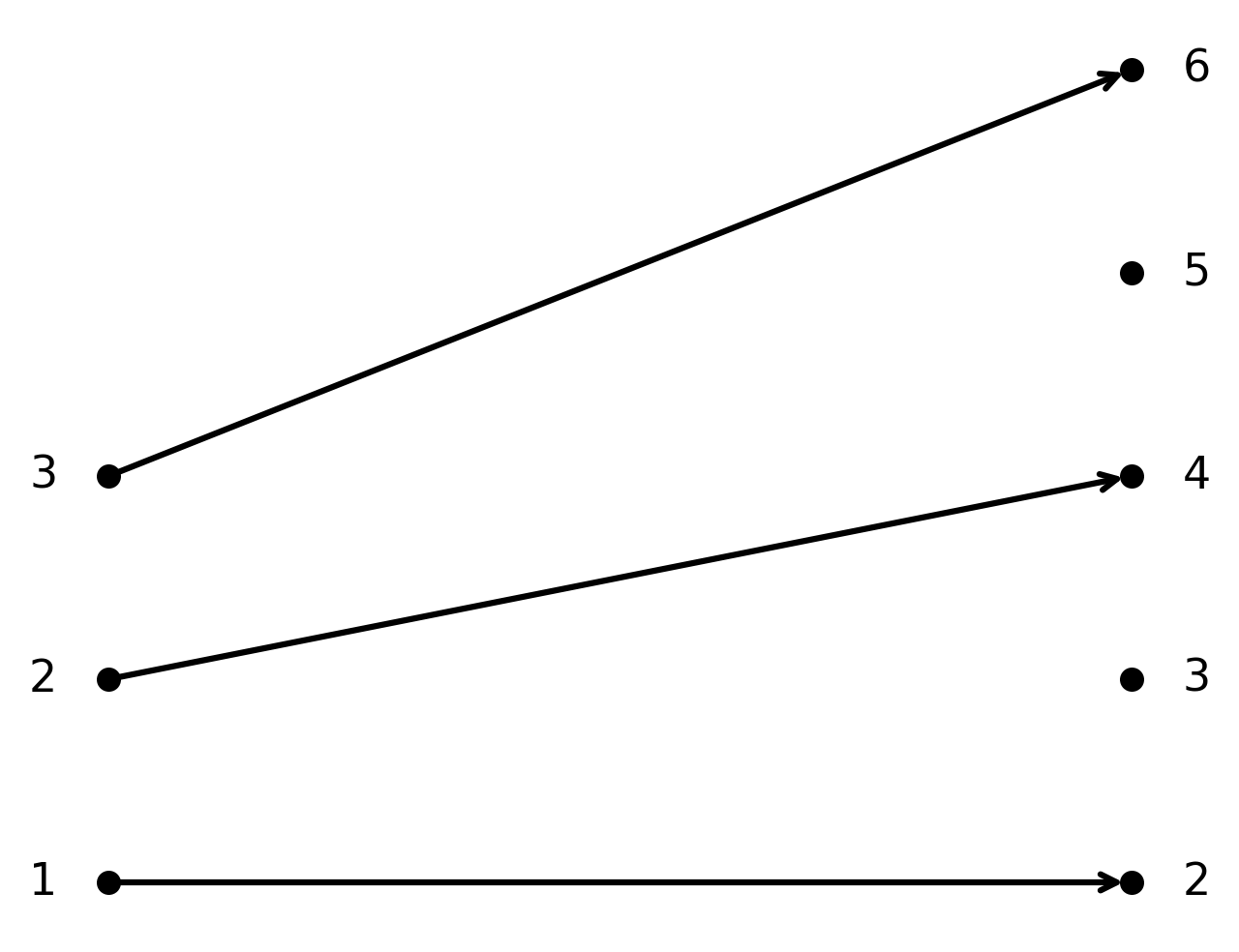
Ici \( f\) est injective, car deux nombres naturels différents donnent toujours des résultats différents lorsqu’ils sont multipliés par 2. Mais la fonction n’est pas surjective, puisque les nombres impairs ne sont pas atteints.

 

 

Exemple 2 : Fonction surjective dans \( \large \mathbb{Z}\)

La fonction \( \large f : \mathbb{Z} \to \mathbb{Z}\) définie par \( \large f(n) = \lfloor \frac{n}{2} \rfloor\).

 

$$ \large f(n) = \left\lfloor \frac{n}{2} \right\rfloor $$

 

 

 

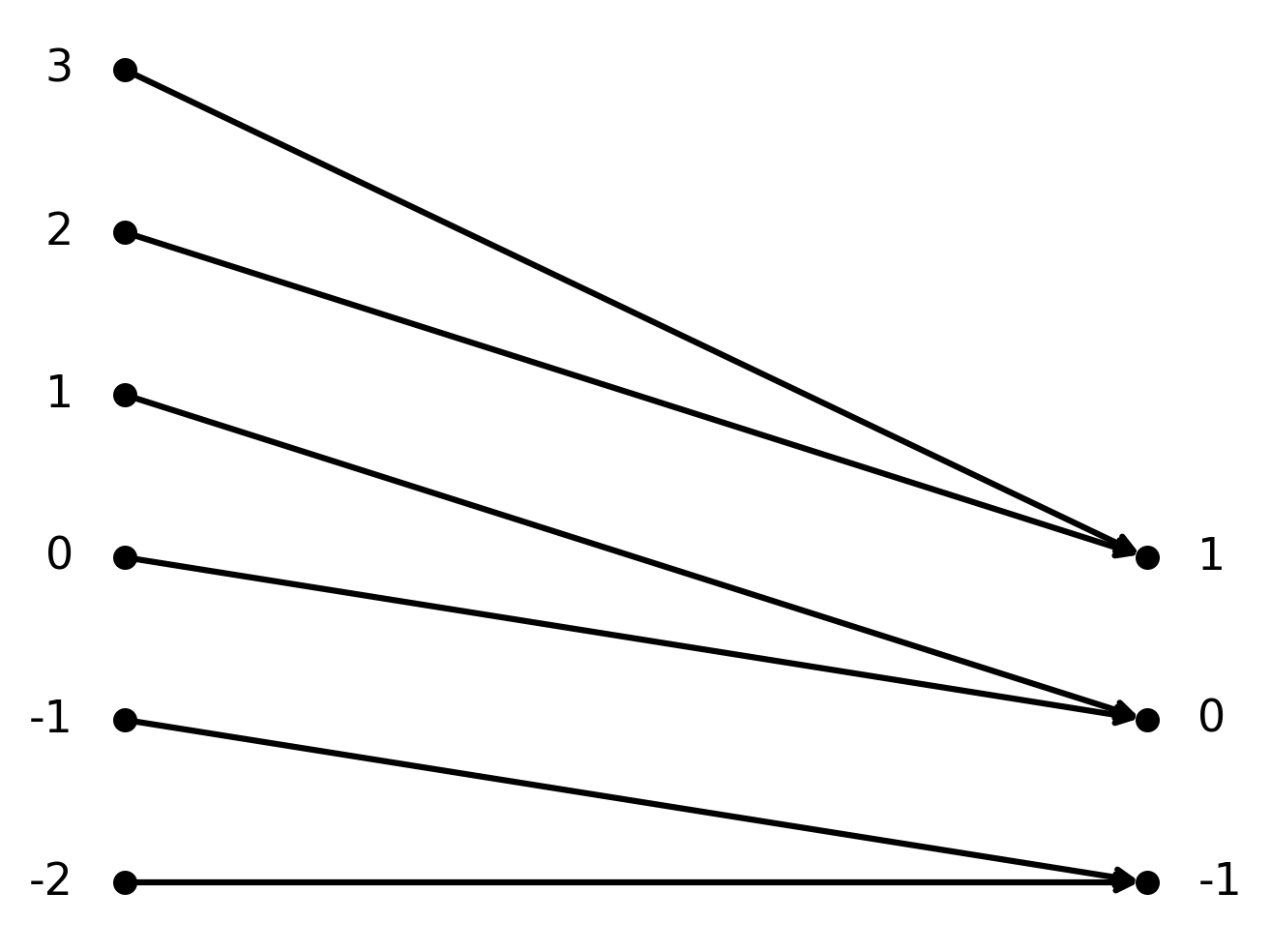
Ici la fonction est surjective, car chaque entier est atteint par au moins un \( \large n\). Par exemple, \(\large f(2)=1\) et \(\large f(3)=1\).

En revanche, la fonction n’est pas injective, car plusieurs entrées peuvent donner la même sortie.

 

 

Exemple 3 : Fonction bijective dans \( \large \mathbb{Z}\)

La fonction \( \large f : \mathbb{Z} \to \mathbb{Z}\) définie par \( \large f(n) = n+1\).

 

$$ \large f(n) = n+1 $$

 

 

Ici \(\large f\) est bijective : chaque entier a une sortie unique et tous les entiers sont atteints.

Ainsi, la fonction peut être inversée avec une inverse \(\large f^{-1}(n) = n-1\).

 

 

Exemple 4 : Fonctions dans \( \large \mathbb{R}\)

Dans les nombres réels, on peut trouver de nombreuses fonctions qui illustrent les propriétés :

 

• \( \large f(x) = x^3 \) de \( \large \mathbb{R} \to \mathbb{R}\) est bijective. Chaque nombre réel a une image unique et tout \( \large \mathbb{R}\) est couvert.
• \( \large f(x) = x^2 \) de \( \large \mathbb{R} \to \mathbb{R}\) n’est pas injective (car \( f(2)=f(-2)\)), mais elle est surjective si l’on considère seulement \( \large [0,\infty[\) comme codomaine.
• \( \large f(x) = e^x \) de \( \large \mathbb{R} \to (0,\infty)\) est bijective, car tous les nombres réels positifs sont atteints de manière unique.

 

 

Résumé

Les exemples montrent que les propriétés des fonctions dépendent de :

 

• Quels ensembles nous considérons comme domaine et codomaine.
• Comment la fonction relie l’entrée et la sortie.

 

Les ensembles numériques classiques \( \large \mathbb{N}, \mathbb{Z}, \mathbb{R}\) fournissent de nombreux exemples simples et utiles de fonctions injectives, surjectives et bijectives.