Fonctions injectives, surjectives et bijectives
En mathématiques, les fonctions peuvent avoir différentes propriétés selon la manière dont les éléments du domaine et du codomaine sont reliés.
Les trois plus importantes sont injective, surjective et bijective.
Fonction injective
Une fonction \( \large f : A \to B\) est injective si deux éléments différents de \( \large A\) ont toujours des images différentes dans \( \large B\).
Autrement dit :
$$ \large f(a_1) = f(a_2) \;\Rightarrow\; a_1 = a_2 $$
Exemple :
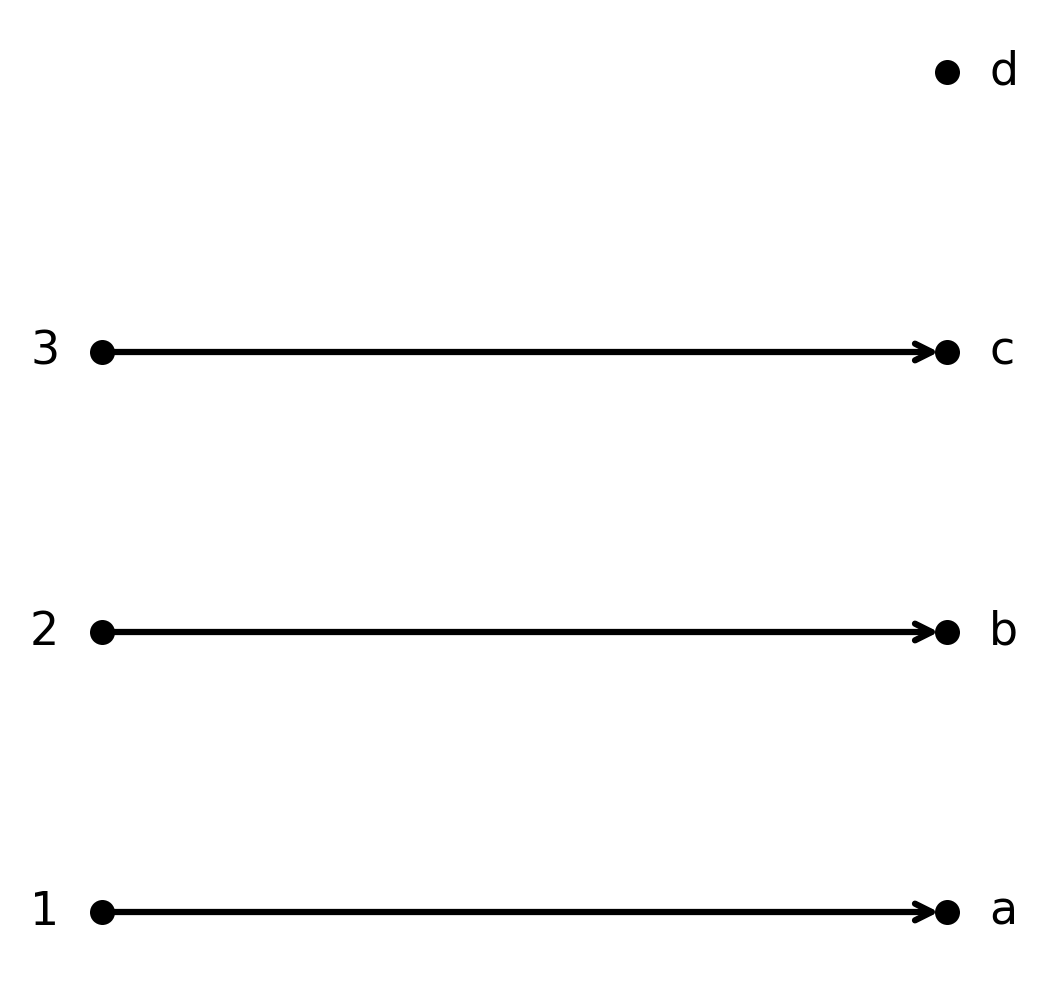
La fonction \( \large f : \{1,2,3\} \to \{a,b,c,d\}\) définie par \( \large f(1)=a, f(2)=b, f(3)=c\) est injective.
Chaque élément de \( \large A\) est associé à un élément unique de \( \large B\), mais tout le codomaine n’est pas couvert.
Fonction surjective
Une fonction \( \large f : A \to B\) est surjective si chaque élément de \( \large B\) est atteint par au moins un élément de \( \large A\).
C’est-à-dire :
$$ \large \forall b \in B, \;\exists a \in A : f(a) = b $$
Exemple :
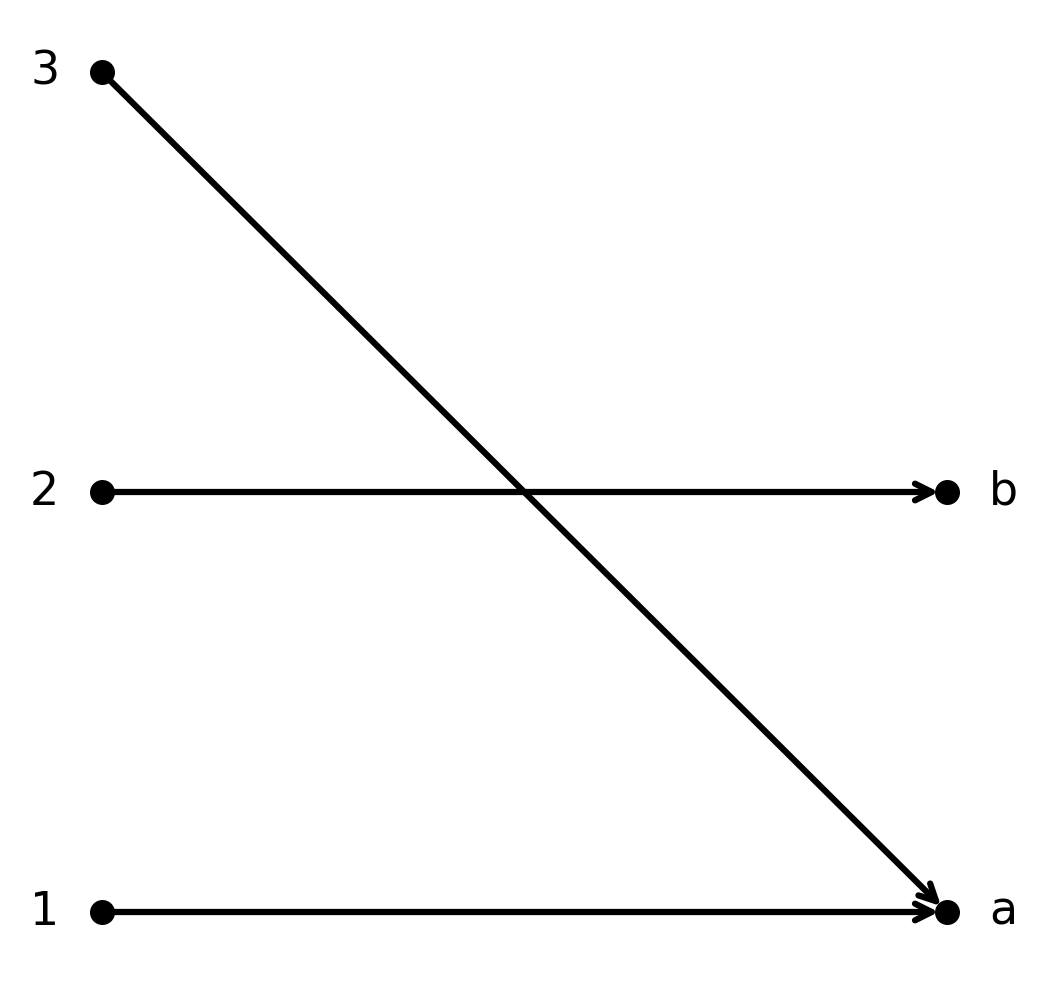
La fonction \( \large f : \{1,2,3\} \to \{a,b\}\) définie par \( \large f(1)=a, f(2)=b, f(3)=a\) est surjective.
Les deux éléments de \( \large B\) sont atteints, mais la fonction n’est pas injective car \( \large 1\) et \( \large 3\) se rapportent tous deux à \( \large a\).
Fonction bijective
Une fonction est bijective si elle est à la fois injective et surjective.
Cela signifie qu’il existe une correspondance biunivoque entre les éléments de \( \large A\) et \( \large B\). Chaque élément de \( \large A\) est associé à un élément unique de \( \large B\), et tout \( \large B\) est couvert.
Exemple :
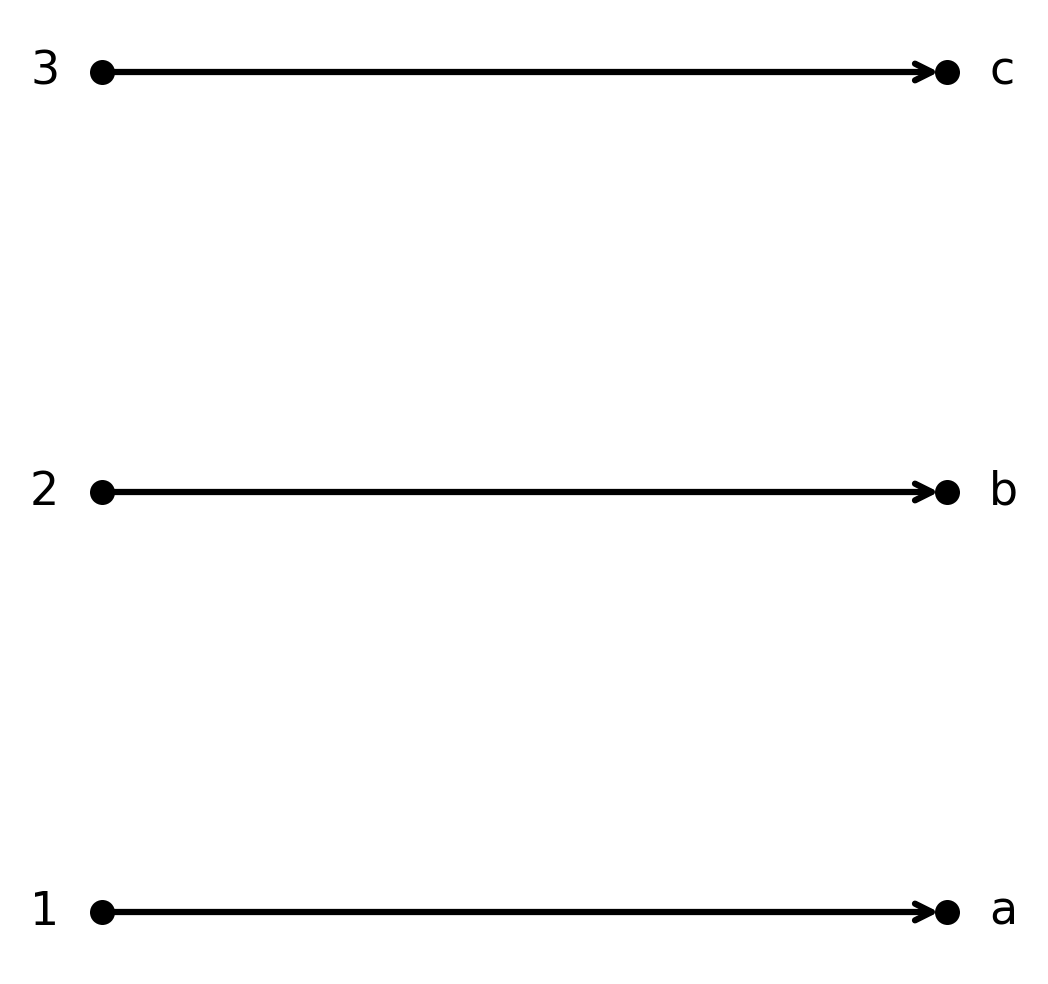
La fonction \( \large f : \{1,2,3\} \to \{a,b,c\}\) définie par \( \large f(1)=a, f(2)=b, f(3)=c\) est bijective.
Chaque élément de \( \large A\) est associé à un élément unique de \( \large B\), et tous les éléments de \( \large B\) sont atteints.
Résumé
- Injective : Deux entrées différentes donnent toujours des sorties différentes.
- Surjective : Tout le codomaine est couvert.
- Bijective : Combinaison des deux – il existe une correspondance biunivoque, qui peut être inversée.
Les fonctions bijectives sont particulièrement importantes car elles ont toujours une fonction inverse, ce qui permet de revenir de la sortie à l’entrée.