Produit cartésien en deux et plusieurs dimensions

Le produit cartésien est une façon de combiner des ensembles pour former des couples ordonnés ou des tuples. Le nom vient du mathématicien français René Descartes (latin : Cartesius), car le concept est à la base des systèmes de coordonnées et de la représentation géométrique des points.

 

 

Produit cartésien de deux ensembles

Si nous avons deux ensembles \( \large A\) et \( \large B\), leur produit cartésien est l'ensemble de tous les couples ordonnés où le premier élément provient de \( \large A\) et le deuxième de \( \large B\) :

 

$$ \large A \times B = \{(a,b) \mid a \in A, \; b \in B\} $$

 

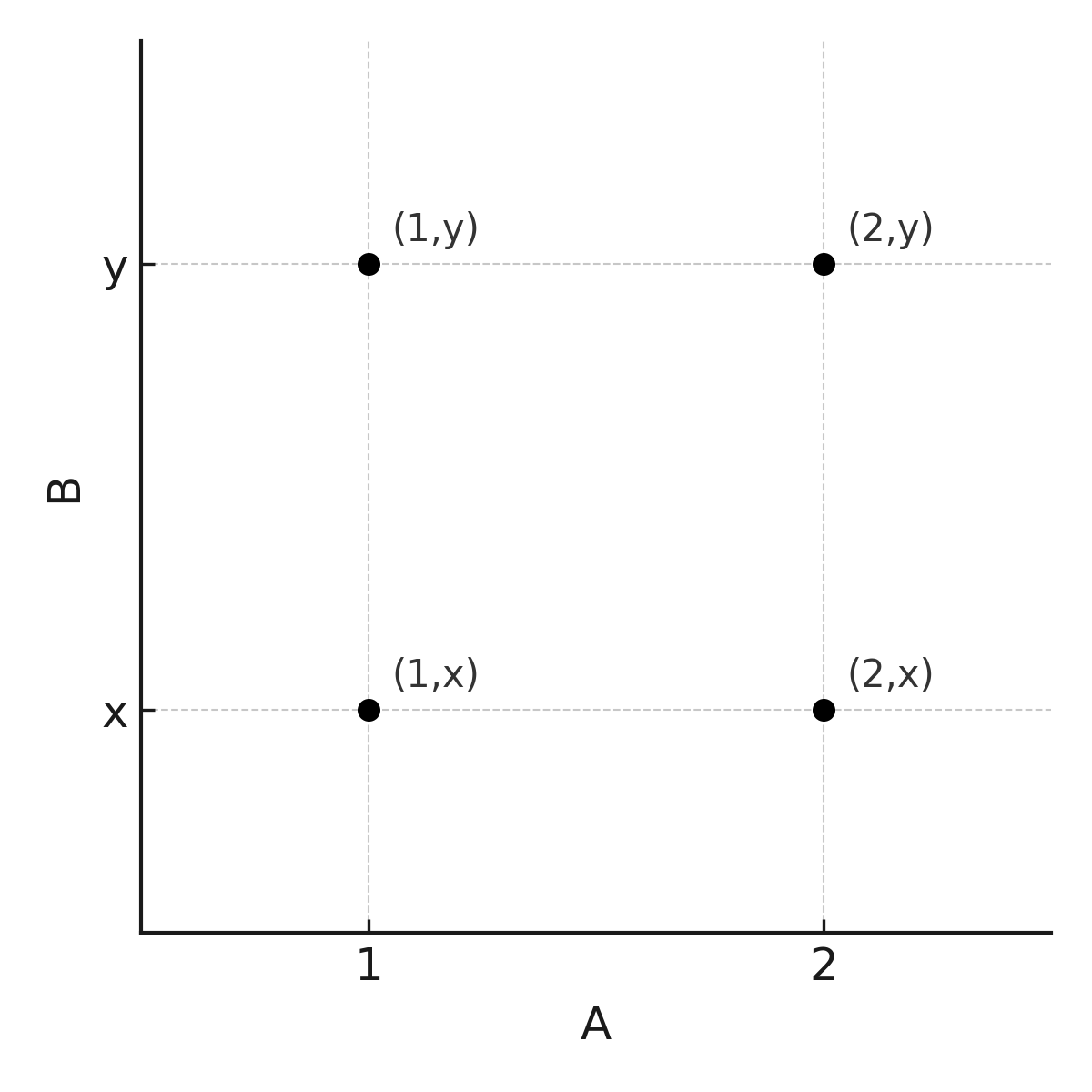
Exemple : Soit \( \large A = \{1,2\}\) et \( \large B = \{x,y\}\). Alors :

 

$$ \large A \times B = \{(1,x), (1,y), (2,x), (2,y)\} $$

 

 

 

 

Remarque : L'ordre a de l'importance. L'ensemble \( \large B \times A\) est :

 

$$ \large B \times A = \{(x,1),(x,2),(y,1),(y,2)\} $$

 

Donc, en général : \( \large A \times B \neq B \times A\).

 

La cardinalité (nombre d'éléments) du produit est donnée par :

 

$$ \large |A \times B| = |A| \cdot |B| $$

 

Exemple : Si \( \large |A|=3\) et \( \large |B|=4\), alors \( \large A \times B\) contient \( \large 3 \cdot 4 = 12\) couples ordonnés.

 

 

Produit cartésien en dimensions supérieures

L'idée peut être étendue à trois ensembles ou plus. Pour trois ensembles, il est défini comme :

 

$$ \large A \times B \times C = \{(a,b,c) \mid a \in A, \; b \in B, \; c \in C\} $$

 

Exemple : Si \( \large A = \{1,2\}, B = \{x\}, C = \{p,q\}\), alors :

 

$$ \large A \times B \times C = \{(1,x,p), (1,x,q), (2,x,p), (2,x,q)\} $$

 

En général, on peut définir un produit cartésien de \( \large n\) ensembles, qui contient tous les \( \large n\)-uples où chaque élément provient d'un des ensembles. Si tous les ensembles sont identiques, par exemple \( \large A \times A \times \cdots \times A\) (avec \( \large n\) répétitions), cela s'écrit \( \large A^n\).

 

Exemples :

 

• \( \large \mathbb{R}^2\) : tous les points du plan, écrits comme \((x,y)\).
• \( \large \mathbb{R}^3\) : tous les points de l'espace, écrits comme \((x,y,z)\).
• \( \large \{0,1\}^3\) : tous les triplets binaires, c'est-à-dire \( \large (0,0,0),(0,0,1),\ldots,(1,1,1)\).

 

Le nombre d'éléments dans un produit cartésien d'ensembles finis est :

 

$$ \large |A_1 \times A_2 \times \cdots \times A_n| = |A_1| \cdot |A_2| \cdot \ldots \cdot |A_n| $$

 

 

Importance et applications

Les produits cartésiens offrent une manière systématique de construire de nouvelles structures à partir d'ensembles connus.

Ils sont à la base de :

 

• Les systèmes de coordonnées en mathématiques et en géométrie.
• Les tableaux et structures de données en informatique.
• Les relations entre objets (par ex., graphes).