Un trapèze est un quadrilatère dont deux côtés sont parallèles. Les côtés parallèles sont appelés bases.

Si les deux autres côtés sont également parallèles, la figure est un parallélogramme. Les côtés non parallèles sont appelés côtés obliques.

Variantes

Trapèze isocèle : \(b=d\). Les angles à la base de chaque côté parallèle sont égaux deux à deux, et les diagonales sont de même longueur.

Trapèze rectangle : Deux des angles sont droits.

Propriétés

• La somme des angles intérieurs est 360°.
• le long de chaque côté oblique on a \( \angle A + \angle D = 180^\circ \) et \( \angle B + \angle C = 180^\circ \) (parallélisme).
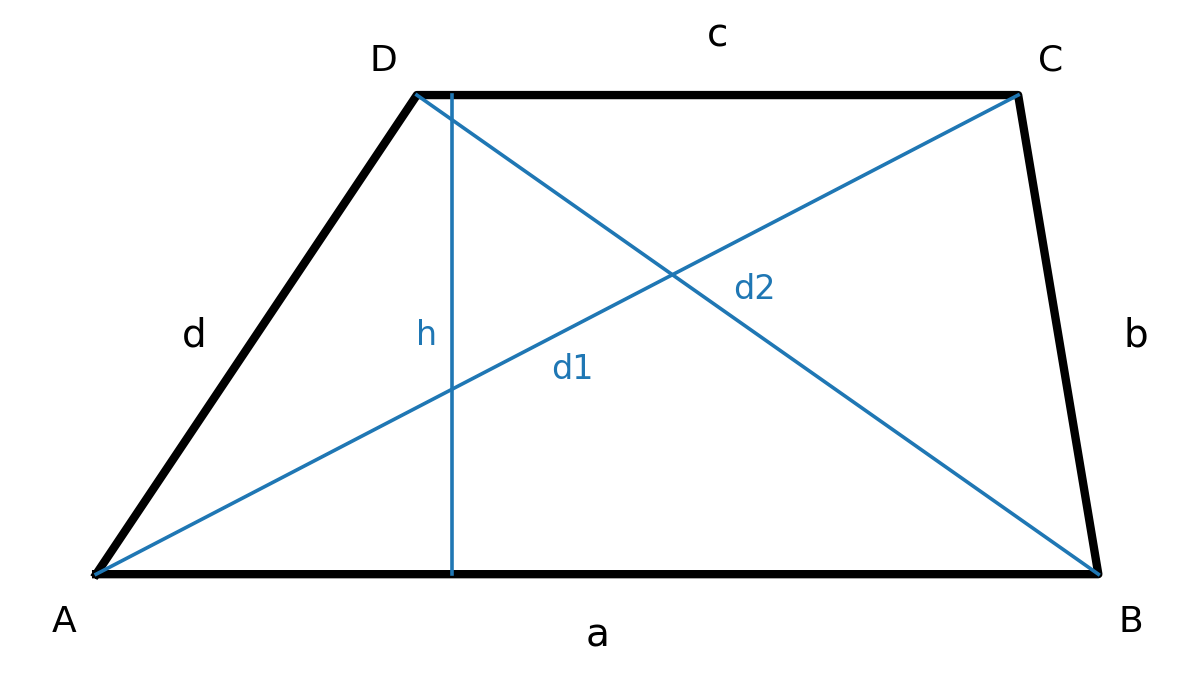
• La médiane (la ligne reliant les milieux des côtés obliques) a pour longueur \( m=\tfrac{a+c}{2} \), et l’aire peut s’écrire \( A=m\cdot h \).

Aire et périmètre

Formule standard pour l’aire :

$$ \large A=\tfrac{h}{2}\,(a+c) $$

Si les angles à la base en \(A\) et \(B\) sont connus, les longueurs des côtés obliques s’écrivent \( d=\tfrac{h}{\sin(\angle A)} \) et \( b=\tfrac{h}{\sin(\angle B)} \). Ainsi, le périmètre est:

$$ \large P = (a+c) + h\!\left(\tfrac{1}{\sin(\angle A)}+\tfrac{1}{\sin(\angle B)}\right) $$

Aire à partir des quatre côtés

Si les quatre côtés sont connus, on peut trouver la hauteur et donc l’aire sans angles :

$$ \large A = \tfrac{1}{2}(a+c)\,\sqrt{\,b^2 - \Bigl(\tfrac{(a-c)^2 + b^2 - d^2}{2(a-c)}\Bigr)^2} $$

On suppose ici \(a \ne c\). Pour un parallélogramme, on prend la limite \(a \to c\).

Diagonales

Les diagonales se trouvent avec la loi des cosinus dans les triangles correspondants :

$$ \large d_1 = \sqrt{a^2 + b^2 - 2ab\cos(\angle B)} $$

$$ \large d_1 = \sqrt{c^2 + d^2 - 2cd\cos(\angle D)} $$

$$ \large d_2 = \sqrt{a^2 + d^2 - 2ad\cos(\angle A)} $$

$$ \large d_2 = \sqrt{b^2 + c^2 - 2bc\cos(\angle C)} $$

Dans un trapèze isocèle, on a \(d_1=d_2\).

Cercle circonscrit

Seuls les trapèzes isocèles peuvent être inscrits dans un cercle. Équivalent : la somme des angles opposés vaut :

• \(\angle A + \angle C = 180^\circ\)
• \(\angle B + \angle D = 180^\circ\)

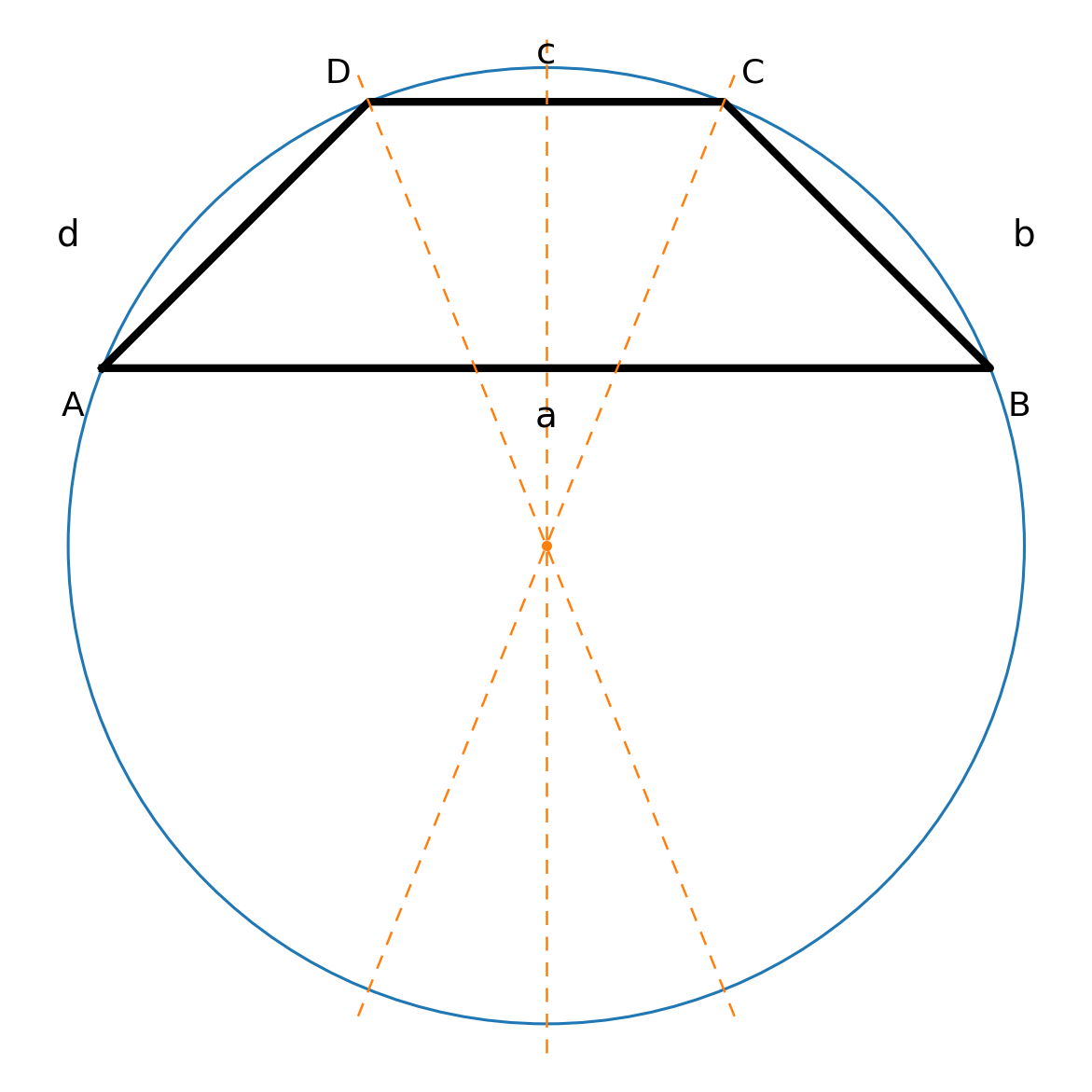
Le centre du cercle peut être trouvé en traçant les bissectrices des angles C et D, et éventuellement la médiatrice des côtés a et c (axe de symétrie).

Remarque : pour tout trapèze, \( \angle A + \angle D = 180^\circ \) et \( \angle B + \angle C = 180^\circ \) en raison des lignes parallèles. Cela ne le rend pas circulaire par lui-même.

Cercle inscrit

Un trapèze possède un cercle inscrit qui touche les quatre côtés si et seulement si :

$$ \large a + c = b + d $$

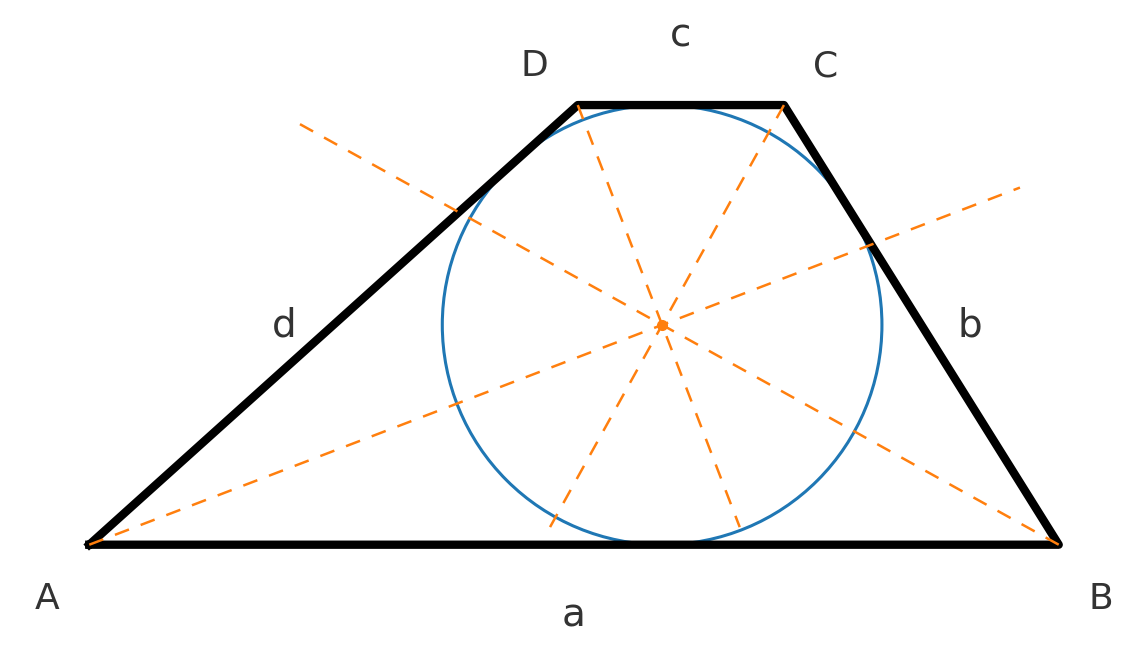
Le centre du cercle peut être trouvé en traçant les bissectrices des quatre angles.

Pour les quadrilatères tangentiel, on a également \( A = r \cdot s \), où \( r \) est le rayon du cercle inscrit et \( s \) est le demi-périmètre.

Applications

• La division en deux triangles rectangles plus un rectangle rend les constructions et les calculs trigonométriques plus clairs.
• La règle du trapèze est utilisée pour l’approximation numérique des intégrales.