Quand on dit quadrilatère, la plupart des gens pensent d’abord à un carré ou à un rectangle. Ces deux figures rectangles se voient partout.

C’est ton écran d’ordinateur, un terrain de football, une feuille de papier A4, etc.

Commun à tous les quadrilatères est que la somme des angles est \(360^\circ\)

$$ \Large \angle A + \angle B + \angle C + \angle D = 360^\circ $$

Rectangle

Un rectangle est un quadrilatère dont tous les angles sont de 90 degrés. Cela signifie que les côtés sont parallèles.

Carré

Si les quatre côtés sont de la même longueur, on l’appelle un carré. Ainsi, un carré est aussi un rectangle et donc les mêmes règles de calcul s’appliquent.

Calcul

Pour un rectangle il est normalement nécessaire de connaître les deux côtés afin de calculer le périmètre et l’aire. À moins que ce soit un carré, alors un côté suffit, puisqu’ils sont égaux.

Mais si l’on connaît la diagonale, on peut diviser le quadrilatère en deux triangles rectangles, ce qui donne d’autres possibilités de calcul.

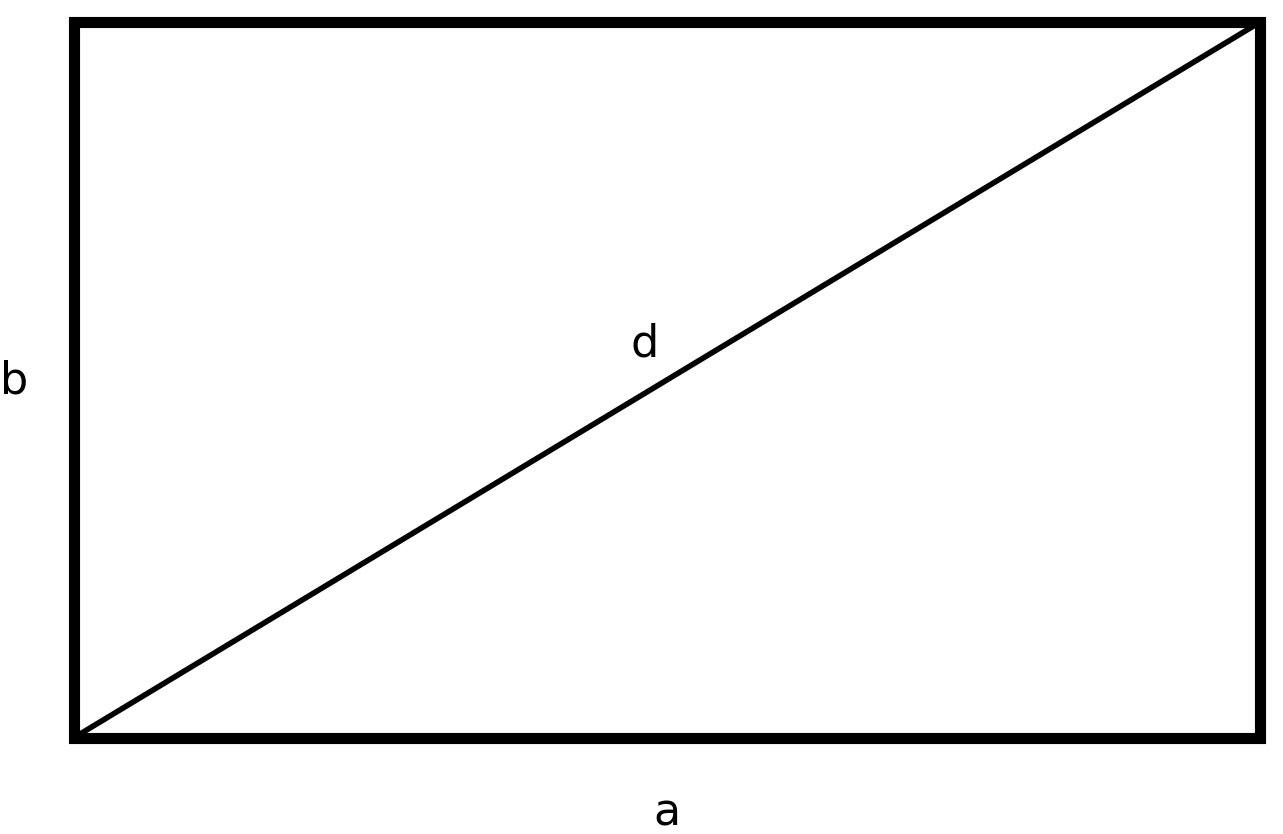
Si tu as appris les équations, tu peux inverser les formules et calculer les côtés, à condition de connaître l’aire ou le périmètre.