Losange
Un losange est un carré incliné et ressemble beaucoup à un parallélogramme, qui est un rectangle incliné.
On peut aussi dire que tous les carrés sont des losanges, mais que tous les losanges ne sont pas des carrés, car les angles d’un losange n’ont pas forcément 90 degrés.
Le losange est souvent facile à calculer en pratique, car tous ses côtés sont de même longueur, comme dans un carré.
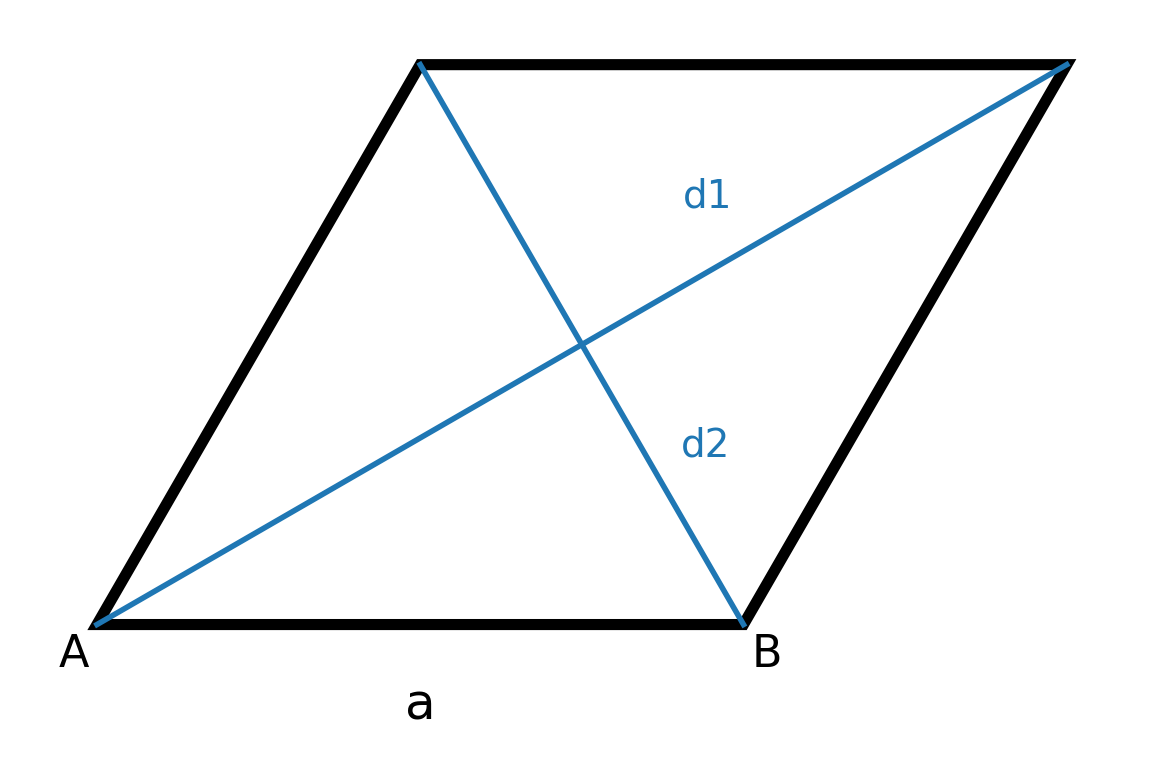
Propriétés qui caractérisent un losange
- Les quatre côtés sont de même longueur.
- Les côtés opposés sont parallèles.
- Les angles opposés sont égaux et les angles adjacents font ensemble 180 degrés.
- Le point d’intersection des diagonales est aussi leur point médian.
- Les diagonales sont perpendiculaires entre elles.
- Chaque diagonale bisecte les angles adjacents, de sorte que la figure a deux axes de symétrie le long des diagonales.
- Le losange peut être divisé en quatre triangles rectangles congruents.
Le fait que les diagonales se bisectent et soient perpendiculaires signifie que le losange peut être divisé en triangles rectangles.
Cela permet d’utiliser le théorème de Pythagore et la trigonométrie élémentaire dans les calculs.