Producto cartesiano en dos y más dimensiones
El producto cartesiano es una manera de combinar conjuntos para formar pares ordenados o tuplas. El nombre proviene del matemático francés René Descartes (latín: Cartesius), porque el concepto constituye la base de los sistemas de coordenadas y de la representación geométrica de puntos.
Producto cartesiano de dos conjuntos
Si tenemos dos conjuntos \( \large A\) y \( \large B\), su producto cartesiano es el conjunto de todos los pares ordenados donde el primer elemento proviene de \( \large A\) y el segundo de \( \large B\):
$$ \large A \times B = \{(a,b) \mid a \in A, \; b \in B\} $$
Ejemplo: Sea \( \large A = \{1,2\}\) y \( \large B = \{x,y\}\). Entonces:
$$ \large A \times B = \{(1,x), (1,y), (2,x), (2,y)\} $$
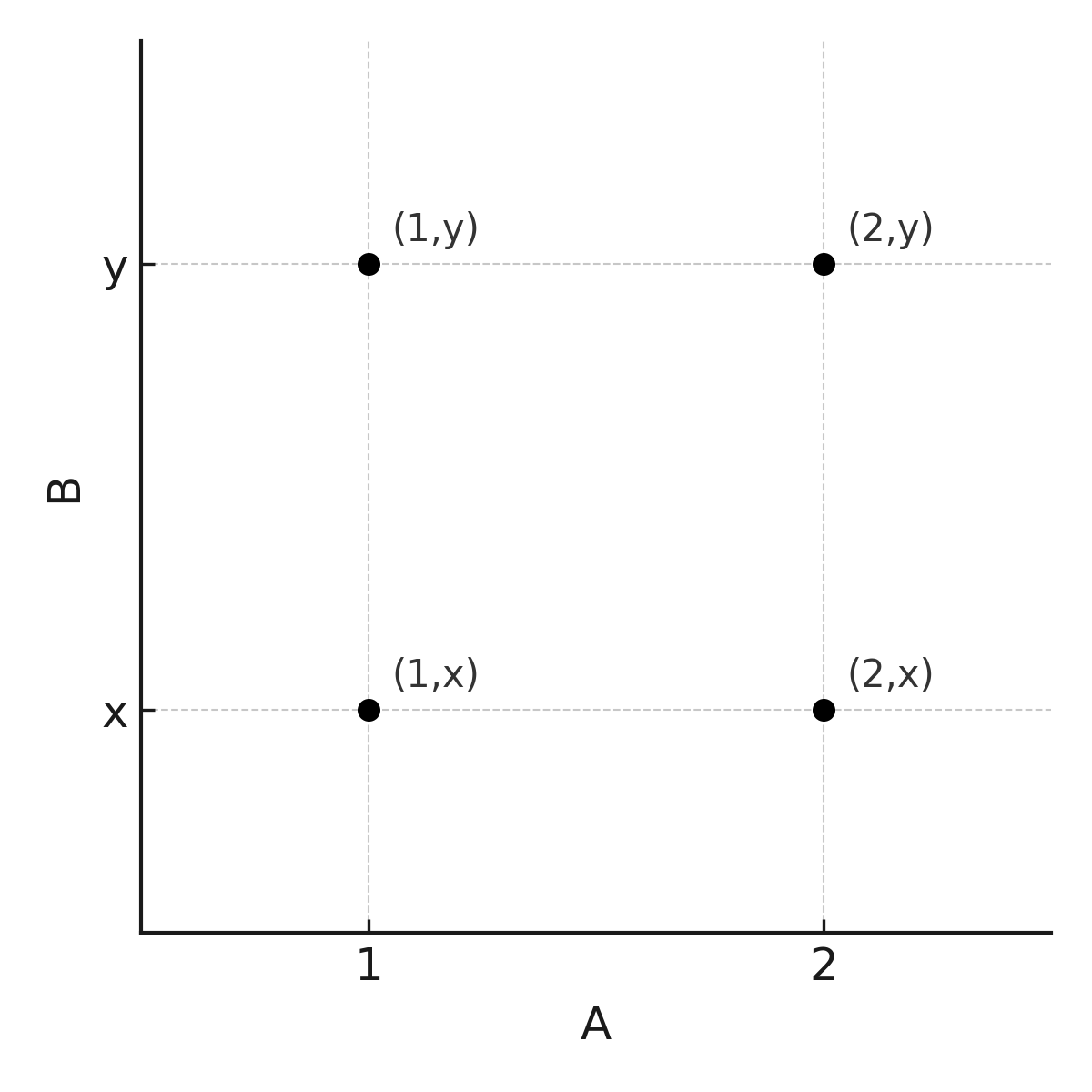
Nota: El orden importa. El conjunto \( \large B \times A\) es:
$$ \large B \times A = \{(x,1),(x,2),(y,1),(y,2)\} $$
Por lo tanto, en general: \( \large A \times B \neq B \times A\).
La cardinalidad (número de elementos) del producto está dada por:
$$ \large |A \times B| = |A| \cdot |B| $$
Ejemplo: Si \( \large |A|=3\) y \( \large |B|=4\), entonces \( \large A \times B\) contiene \( \large 3 \cdot 4 = 12\) pares ordenados.
Producto cartesiano en dimensiones superiores
La idea puede extenderse a tres o más conjuntos. Para tres conjuntos se define:
$$ \large A \times B \times C = \{(a,b,c) \mid a \in A, \; b \in B, \; c \in C\} $$
Ejemplo: Si \( \large A = \{1,2\}, B = \{x\}, C = \{p,q\}\), entonces:
$$ \large A \times B \times C = \{(1,x,p), (1,x,q), (2,x,p), (2,x,q)\} $$
En general, se puede definir un producto cartesiano de \( \large n\) conjuntos, que contiene todas las \( \large n\)-tuplas donde cada elemento proviene de uno de los conjuntos. Si todos los conjuntos son iguales, por ejemplo \( \large A \times A \times \cdots \times A\) (con \( \large n\) repeticiones), se escribe como \( \large A^n\).
Ejemplos:
- \( \large \mathbb{R}^2\): todos los puntos en el plano, escritos como \((x,y)\).
- \( \large \mathbb{R}^3\): todos los puntos en el espacio, escritos como \((x,y,z)\).
- \( \large \{0,1\}^3\): todas las ternas binarias, es decir, \( \large (0,0,0),(0,0,1),\ldots,(1,1,1)\).
El número de elementos en un producto cartesiano de conjuntos finitos es:
$$ \large |A_1 \times A_2 \times \cdots \times A_n| = |A_1| \cdot |A_2| \cdot \ldots \cdot |A_n| $$
Importancia y aplicaciones
Los productos cartesianos proporcionan una manera sistemática de construir nuevas estructuras a partir de conjuntos conocidos.
Constituyen la base de:
- Sistemas de coordenadas en matemáticas y geometría.
- Tablas y estructuras de datos en informática.
- Relaciones entre objetos (p. ej., grafos).